A. R. Jensen, Reviewer' Comment, sent to the Editor in Chief H. J. Eysenck, July 1991:

"Whether Weiss' s theory is true or false, which remains a very open question at present, this article seems to me an impressive effort that deserves full exposure to a wide audience. ... In fact, this is the first article I' ve read on a major gene theory of g that has made me think there might possibly be something to it. If it were adequately proved, of course, it would be a truly major advance."

Published in: Personality and individual Differences 13 (1992) 1115-1134

Home

Content

• SUMMARY

• INTRODUCTION

• THE RELATIONSHIP BETWEEN MATHEMATICAL GIFTEDNESS AND GENERAL INTELLIGENCE

• MAJOR GENES AGAINST POLYGENES AND OTHER CURRENT ASSUMPTIONS

• TOWARD THE DETERMINATION OF IQ IN CELL CULTURE

• THE EVOLUTION OF A BALANCED POLYMORPHISM FOR HUMAN INTELLIGENCE

• ACKNOWLEDGEMENT

• REFERENCES

Summary. - Evidence in favour of the major gene theory of intelligence is stated in summary form. Empirical distributions from studies on giftedness by Terman and Weiss and data of social mobility can be explained by the existence of a major gene that in the homozygous state is the prerequisite to have an IQ of 130 or higher. Under the assumption of about 10% misclassification of genotypes, family data are in agreement with Mendelian segregation at such a major gene locus. Elementary cognitive tasks, highly correlated with IQ, are not distributed normally. On the absolute scale of short-term memory capacity (measured in bits), defined as the product of memory span and mental speed, the heterozygotes are intermediate between the homozygotes. Where there are major genes, there must be an underlying biochemical code, which can be detected. To this aim enzymes, responsible for the regulation of brain energy metabolism and correlated with IQ and social status, should be the target of further research. From the point of view of evolution, social stratification and the frequency of major genes of intelligence depend upon each other.

Beginning in 1972 (Weiss, 1972), the author has published a series of papers (Weiss, 1973, 1979a; Weiss and Mehlhorn, 1982) and even a monograph (Weiss, 1982a), whose main content were arguments and empirical evidence in favour of a major gene locus of general intelligence. This line of reasoning, based on empirical facts, was underpinned by papers, stressing the theoretical (Weiss, 1974, 1978) and historical aspects of the problem (Weiss, 1980, 1982b). The disadvantage of all these publications was, due to the enforced provincialism of former East German science (Weiss, 1991), that the empirical starting point (Weiss, 1972, 1973) of the logical thread of all arguments was until now only available in German and, therefore, for English readers, the arguments published later (Frank, 1985; Weiss, 1986; Weiss, Lehrl and Frank, 1986; Weiss under the pseudonym Weisman, 1988), are based on loose ground. Therefore, the author is glad to follow an invitation by the editor ) of this journal to write a paper "setting out all the arguments for the major gene theory of intelligence. This is not really available to English readers, but I think it goes so much against current assumptions that the argument and the evidence in favour should be stated in summary form, but giving enough of the evidence for people not to have recourse to German publications." (H. J. Eysenck, letter of February 14, 1991)

In 1969 Hans Grimm, at this time head of the Institute of Physical Anthropology of the Humboldt-University at Berlin (East), proposed to the author to carry out an empirical investigation into the family background of mathematical giftedness. Grimm was well aware (Grimm, 1943) that the archives of some foundations for the promotion of the gifted would provide a wealth of data. From 1963 to 1971 about 2,800, 000 East German school children participated in nine nation-wide mathematical competitions (Engel, Pirl and Titze, 1971). In the first stage of the selection process, repeated each year in each school, nearly all mentally normal students of an age between 10 and 18 years took part.

The second and third stages were organized at district and county levels, respectively. The fourth stage, a two-day paper-and-pencil-examination under close supervision and restricted to an age between 15 and 18 years and to some younger students who had already excelled the necessary cut-off score, was reached by the 1329 most successful participants of the third stage at least once, by many of them several times. In terms of psychometry this selection process fulfilled the requirements of a standardized school achievement test. This is important to the argument of this paper as in East Germany IQ testing was officially forbidden (compare for background information Weiss, 1991) and for that reason it was quite impossible to administer IQ tests to the probands and their relatives. In order to get data about the background of the gifted, questionnaries were distributed to their parents. We asked a sample of the parents not only to fill in their jobs and occupations, and their achievements in school and life, but requested this information also for all relatives of the first and second degree of the probands, for all male relatives of the third degree and moreover for the female cousins of probands and the cousins of the parents. Altogether, from 524 returned questionnaires and from the filing cards of the 1329 probands we obtained data on about 20,000 individuals.

From the high degree of selection we could conclude that the IQ of probands should be 130 or higher. Test scores of mathematical achievement and of general intelligence are always highly correlated (compare Table 1). The same holds for correlations with overall school achievement and with social status. In 1980 in a representative sample (n = 936) of East German school children of age 11, subjects with an IQ (tested with Raven` s Progressive Matrices) of 143 had in school in mathematics (the population mean was 2.7) marks with a mean of 1.3, with IQ 107 a mean of 2.4, with IQ 88 a mean of 3.4 (for more details see Weiss, 1982a, p. 94). No other single special field was as highly correlated with IQ as mathematics. And those who are conspicuous in mathematics, are also far above average in other special subjects (with the exception of music, drawing and physical exercise; of which was already aware Spearman in 1904).

The filing cards of the probands reflected also their professional aspirations to get university degrees as mathematicians, physicists, engineers, and as experts in financing. In a first follow-up study (Haenschke, 1985; Pollmer, 1989) it could be confirmed that 92% of all probands in fact did get such a degree; plus 7%, who got a degree in non-mathematically oriented fields (as medicine, biology or the humanities). Considering the 92% of correct classification by profession alone and using a more conventional terminology, we could also speak of a penetrance(1) of 0.92. Only 1% did get no degree at all. Already in school and high-school 97% of all probands were far above average, and even 64% got mark 1 in all or nearly all subjects of the high-school leaving examinations (i.e. the German "Abitur" with mark 1).

In 1983 (Pollmer, 1989) 62% of all probands held jobs at the universities, in computer centers and other research institutions. Whereas one half of all probands excelled in creativity by obtaining patents for inventions and honours for discoveries, the other half did not. (A deeper investigation into the personality differences between two possible comparison groups, one group of extreme creativity, the other without, given the same level of IQ and both groups matched by social background, was planned in the follow-up study in 1982, but was made impossible by the political situation in former East Germany (see Weiss, 1991)). To say it in another way: For a high level of creativity in science and engineering a high level of IQ is necessary and from such a creativity in these fields a high IQ of a given individual can be inferred. However, the reverse conclusion from non-creativity to a lower IQ is not allowed. One of the byproducts of the empirical data was also that the top performers in field as biology, medicine, management, and the humanities, where the mean IQ is generally lower, are also within an IQ-range of 130 or higher. In such a way the probands could be characterized as a relatively homogenous group in jobs and professions always ranking at the top of IQ classifications (e.g. Stewart, 1947). The only obvious difference was for students of medicine: In former East Germany the physicians had a much lower income than in Western countries and therefore this profession was not as attractive and, hence, their rank by IQ as a professional group was relatively lower.

Of the the fathers of the probands 43% also belonged to the same group with highly qualified professions as the 92% of the probands themselves, already mentioned above; additionally 24% of the fathers got university degrees in less mathematically oriented fields (compared to 7% among the probands). 25.5% of the fathers were clerks or skilled workers in jobs such as book-keeper, mechanics, tool fitter and draughtsman, usually ranked with an mean IQ of approx. 110. Only 7.5% of all fathers were skilled workers with jobs such as mason, butcher, electrician or locksmith, usually ranked with an IQ of approx. 100. However, it was remarkable that in nearly all such cases in the questionnaires data were given on above average achievements in school mathematics and in job performance. A locksmith, for example, was alone responsible for a plant and honoured as an innovator. Therefore the conclusion that the IQ of these men was in most cases in the upper range of their respective profession and about 110, seems to be justified. Only 1% of all fathers were unskilled workers. And in most of such cases reasons were given why a professional career had been impossible (for example, diabetes or invalidity as a consequence of World War II). Of course, single cases of illegitimacy could not be excluded. - For the mothers the results were not so clear-cut: alone 37% of them were in jobs, formerly typically done by females, such as secretary, stenotypist, book-keeper, teacher and laboratory assistant and requiring above-average intelligence. Some mothers, were housewifes without any profession, but with a number of children and a high-school leaving examination (Abitur). School-achievement and the confirmed correlation of IQ of about 0.50 (Garrison, Anderson and Reed, 1968) between husband and wife could help to classify even such mothers into a crude IQ-classification (compare Table 2), but in some cases a bit of speculation could not be avoided. We are aware that this is the weakest point of our argument.

The following empirical findings were especially impressive:

(1) In cases where the proband had a father who belonged to the same professional group as 92% of the probands themselves, all sibs of the proband were above average in mental powers . (With two exceptions: one case of eclampsia; one case of Down syndrome.) In such families the mother could be in any profession or be a housewife.

(2) In cases where the proband had a father who did not belong to the same professional group as 92% of the probands, the sibs of the probands could have any job or profession. 14% of all these sibs (see Weiss, 1982a) were in jobs, usually requiring no more than average intelligence. In the questionnaires, in such cases the parents had written expressively "without special interests", "without special achievements", "average achievements", whereas for the probands and other sibs they had given very detailed information about achievements and honours in school and job performance.

(3) Even more impressive was a finding among the collaterals: Parents (i.e. sibs of the parents of the probands and their respective spouses) who both belonged to the extreme high IQ group as the probands, nearly always only had children (i.e. cousins of the probands) of the same far-above average quality. Unskilled parental pairs mostly only had children in unskilled jobs. Parental pairs, where both spouses were in an IQ-range of approx. 110, had children who were scattered over all possible jobs and professions.

By classifying jobs and professions according to their content of general intelligence (compare Gottfredson, 1986), the mentioned empirical findings suggested the following hypothesis: Let us assume, that all the probands and the professional group to which 92% of the probands belong would be homozygous for a Mendelian allele M1 (hence outfitted with the genotype M1M1), the unskilled workers and average IQ jobs would be M2M2, the jobs clustering about a mean IQ of 110 would be heterozygous M1M2. There should be an error of classification between 10 and 20% - compare the 92% of probands which can be classified correctly by nothing else than their given profession - and correct classification is more difficult for women than for men. Misclassification cannot be completely avoided and is a consequence of a large number of biological and social influences (among them effects of other genetic loci and personality factors; disease; accidents; damage during development; social inequality of chances) and lacking or incomplete information based on questionnaires. Obviously, given a misclassification (or penetrance in conventional terminology) between 10% (for males) and 20% (for females), even in cases of M1M1-M1M1 marriages, a 100% M1M1 offspring (also itself with the same possible range of misclassification) cannot expected and the results could only be in a range between 75 and 100% (compare Table 1), for M1M1-M1M2 marriages between 50 and 75%, for M1M2-M1M2 marriages between 25 and 50%, and even for M2M2-M2M2 marriages M1M1 offspring cannot be 0% , but should be between 0 and 25%. (Hence we can characterize regression to the mean as a consequence of error of measurement; in our case here simply as error of classification. In pure homozygote genetic crosses, and not considering the effects of minor genes, there should be no regression to the mean.) When Table 2 was published for the first time (Weiss, 1972) fuzzy concepts and logic were nearly synonymous with unscientific way of arguing, now fuzzy statistics should be better understood.

The terminology of genetics is not always consistent: we can speak of the gene frequency of the allele M1, but we speak of the genotype M1M1. And it is quite correct to speak of major genes instead of alleles of the major gene locus M. The reader should not be disturbed by this, and the author assumes that the facts of Mendelian segregation are common knowledge even among psychologists. That n M1M2-M1M2 marriages with 100 children should segregate theoretically into 25 M1M1, 50 M1M2 and 25 M2M2 children is simply applied probability and combinatorics and not an especially incomprehensible law of nature. Of course, the allele M2 could also be understood as an abstraction and be in reality a series of n alleles with small differences; but with a large difference to the M1 allele or an allele-1 series. And every major gene concept is an abstraction with regard to minor genes and environmental influences (in a broad sense), as is the concept of Spearman` s general intelligence (1904) with regard to broader and more and more fuzzy concepts of intelligence.

The hypothesis of a major gene locus of general intelligence with an autosomal allele M1 in the homozygous state as the prerequisite to have an IQ (100; 15) of 119 and higher was tested in the families of the sibs (i.e., aunts and oncles of the probands) of the parents of the probands. Accordingly, the total numbers in Table 2 are the distribution of the first cousins of the probands.

Monozygotic twins of probands share all their genes with the probands, sibs and parents half of their genes, grandfathers and sibs of parents a fourth, greatgrandfathers and cousins an eigth. Therefore, in cases of classical genetics it is easily possible to draw a conclusion about the underlying gene frequency in the total population from the frequencies of genotypes among the relatives of homozygous probands (Li and Sacks, 1954). Because of historical change of the occupational structure and underlying IQ requirements our non-classical and fuzzy problem is far more complicated. 92% of all probands were in professions, typical for M1M1; 55% (n = 177) of the brothers; 40% (n = 346) of the fathers; 18% (n = 570) of the male cousins; 11% (n = 2250) of the male cousins of the parents; 9% (n = 681) of the grandfathers; 5% (n = 1996) of the uncles of the parents; and 4 % (n = 1290) of the greatgrandfathers (Weiss, 1973). Theoretically, in a classical Mendelian case the percentage among uncles and grandfathers, for example, should be the same, the difference in our data is due to historical change of the occupational structure. (The mean year of birth for the uncles is 1917, for the grandfathers 1887, for the brothers of probands 1947.) By accounting for this change, we estimated that the gene frequency p of the hypothetical major gene M1 of general intelligence is about 0.2 (Weiss, 1973), of the gene M2 the frequency q is about 0.8. From the Hardy-Weinberg-Law of population genetics, where p + 2pq + q = 1, follows 0.04 M1M1, 0.32 M1M2 and 0.64 M2M2. However, assortative marriage for IQ with about r = 0.50 (Garrison, Anderson and Reed, 1968) has the consequence that the percentage of heterozygotes in the total population is reduced, from which follow frequencies of about 5% for M1M1, 27% for M1M2 and 68% for M2M2 (Weiss, 1979a). The medians of the cumulated percentils (M2M2 34; M1M2 81.5; M1M1 97.5) correspond to the following median IQs: M2M2 IQ 94; M1M2 IQ 112; M1M1 IQ 130.

During the last two decades several authors (for example, Stafford, 1972) have again and again advanced hypotheses on an X-chromosome linked inheritance of mathematical or spatial ability. Such claims were supported or rejected by higher correlations betweens mothers and sons and fathers and daughters in contrast to mother-daughter and father-son correlations. Indeed, X-chromosome linked inheritance generates a unique pattern of such correlations, but the evidence in favour or against such linkage remained always contradictory. There are as much confirmations as rejections, and we have not the intention to review these studies here. It is a peculiarity of psychological research and its restrictedness to arguments of mere correlations that the deeper Mendelian approach (Weiss, 1985) has never been tried: in the case of X-linked recessive inheritance of a gene influencing mathematical or spatial ability, male probands scoring very high in such ability (i.e. our M1M1) should have a larger number of male relatives (brothers of the mother; fathers of mothers) on their mothers side who also excel in such abilities than among the relatives of their fathers. There was not the least hint of such deviation in our data, comprising thousands of male relatives on both maternal and paternal side. And since 1972 the hypothesis of X-linked inheritance of factors of mathematical ability should be rejected for all and ever, if the original publication (Weiss, 1972) would have been in English. What was revealed by the questionnaires was a different structure of interests and social values for male and females. Even among our sample of highly gifted subjects, 47% of female probands were interested in belletristics , but only 15% of males were; 68% of the girls could play a musical instrument, but only 31% of the boys could; of which 43% were amateurs in electronics and related fields, but only 11% of the girls were.

What cannot be excluded by our data is that autosomal genes are also regulated and influenced by genes located on sex chromosomes. But this is quite a different story, and (for example, hormonal) regulation of mental traits by sex chromosomes should not be confounded with linkage to such chromosomes. For minor genes of intelligence sex-chromosomal linkage is always a possibility, worthf investigating. For example, because homozygotes with a marker X-chromosome (Howard-Peebles and Stoddard, 1979) are mentally retarded, for the heterozygotes a slight decrease in IQ could be ecpected, analogous to confirmed cases of autosomal syndromes of mental retardation (see Propping, 1989, pp. 322-323). The IQ of heterozygotes for phenylketonuria is reduced of about 5 points.

Recently, Crow (1991) put forward the hypothesis that genes promoting both intelligence and psychosis are located in the pseudoautosomal exchange region of the sex chromosomes. Genes within the region can be transmitted from father to son as well from father to daughter; hence the pattern of transmission is autosomal. The characteristic feature of pseudoautosomal transmission is same sex concordance, that is, that affected siblings (in our case the highly gifted M1M1 probands and their M1M1 sibs) will be more often than would be expected of the same sex. In our questionnaires we counted 143 (142) male-male sibling pairs, 23 (22) female-female and 107 (109) male-female pairs (theoretically expected numbers in parentheses). Considering the difficulty in classifying females as undoubtful M1M1 (10 additionally male-female pairs are doubtful, but only 2 male-male pairs), this result is no deviation from chance; and Crow` s hypothesis must be rejected by our data with regard to general intelligence.

In the monograph by Weiss (1982a; Weiss, Lehrl and Frank, 1986) from the review of the most important family studies of giftedness (Terman and Oden, 1948; Oden 1968), of top scientists (Visher, 1948), top managers (Warner and Abegglen, 1955), top inventors (Rossmann, 1930), famous men (Maas, 1916; Juda 1953) and of top performers in high schools (Rüdin, 1951) the following conclusion could be generalized: an unskilled worker can have a highly gifted grandchild, but has only in very exceptional cases has a highly gifted child. In full accord with a major gene theory of human intelligence, social mobility from one extreme of the social ladder to another needs at least two generations. (A homozygote M2M2 can never procreate a M1M1 child. He has to marry a M1M2 wife, if his grandchild will have a chance to be M1M1.)

Some critics will say, because there was no IQ testing, the results (Weiss, 1972, 1973) cannot be discussed seriously. For Terman (1925), who could select his gifted sample of children (mean IQ 150; cut-off score IQ 140) by testing, administering tests to the parents was not practical. His "Barr scale rating of occupational status" (see Table 3) is methodologically similar to our approach (see also McCall, 1977; Wilson et al. 1978): 20 judges rated a list of 121 representative occupations on a scale of 0 to 100 according to the grade of intelligence which each was believed to demand. The results of table 2 (with mothers included) from communist East Germany and table 3 (only fathers) from classical free-market America should be carefully compared, because they support each other. The children of the Terman-sample (Oden, 1968) had a mean IQ of 132, 34% of them had again an IQ above 140 (i.e., M1M1 I would like to state.) The occupational distribution of the Terman gifted group (see Table 4) is very similar to the distribution of our mathematically gifted (Haenschke, 1985; Pollmer, 1989).

In a study by Wilson et al. (1978) various socioeconomic indexes (compare also Weiss, 1981) and the Hollingshead Occupational Scale (as by McCall, 1977) were used to generate occupational status scores for each subject. Predicted IQ by these scores differed from actually tested IQ l< 5 points in 37% of subjects, < 10 points in 66%, and < 15 points in 88%. Very similar results were obtained by Karzmark et al. (1985) using only years of education. By combining years of education, occupational status and school achievement, our approach (Weiss, 1972 and 1973) should have a comparable range of error.

There are findings which cannot be accounted for by any hypothesis of human genetics: in all larger studies of giftedness (Terman, 1925; Juda, 1953) firstborns were overrepresented. Among mathematically gifted from two-children families were 49 firstborns, 19 secondborns (see Weiss, 1982a). In any social stratum a correlation between IQ and birth rank has been confirmed, i.e. children with birth rank 5 have an IQ of about 10 points lower than firstborns (Gille et. al., 1954). This can only be a phenotypic effect and genetic true scores of healthy laterborns cannot be different from scores of firstborns. True scores are or can also be obscured (see Weiss, 1982a, for citations of relevant studies) by IQ-acceleration, gene frequency fluctuations between generations, deprivation and chronic poisoning by environmental pollution. Husen (1951) could prove that the IQ will be raised in the mean about 5 points by better schooling, by high schools even up to 10 points. If many or all children benefit from better education and more intellectual stimulation, IQ acceleration of the respective population will be the result. Genetic true scores are not altered by such acceleration (Weiss, 1979c). If we speak about social and other environmental influences on IQ, changes of 10 or even 20 points are possible. However, the two homozygote genotypes M1M1 and M2M2 have an IQ difference of about 40 points and no civilized environment brings forth modification in such order of size.

"There are several critical thresholds within the total range of IQ, each having important educational and occupational consequences for the individual. It is largely the layman` s perception of this critical threshold property of intelligence, ... that lends the IQ its importance in the public eye and makes it such a sensitive and controversial topic" (Jensen, 1980, p. 115).

IQ differences smaller than about 10 points are not generally socially perceptible. Beyond the threshold regions of the major genes, the IQ scores becomes relatively unimportant in terms of ordinary occupational aspirations and criteria of success. According to Jensen (1980, p. 114):

"the socially and personally most important threshold regions on the IQ scale are those that differentiate with high probability between persons who because of their level of general mental ability, ... can or cannot succeed in the academic or college preparatory curriculum through high school (about IQ 105), and can or cannot graduate from an accredited four-year college with grades that would gratify for admission to a professional or graduate school (about IQ 115)."

This means, because other stratifications are economically less effective that the structure of the educational and occupational system of modern industrial societies is adapted to the gene frequencies of the major gene locus of general intelligence.

Spearman (1904) and his followers have never tried to confirm the concept of general intelligence in terms of Mendelian genetics. From Spearman`s time until today it is assumed among psychologists that the Mendelian approach is restricted to traits with clearly distinguishable phenotypic classes. But intelligence is, as everybody knows, a quantitative trait being measured on a continuous scale. This is why the reigning biometrical doctrine seeks to measure all the variation in a character and to partition the differences observed into fractions (variances, heritabilities) ascribable to the effects of genetic and environmental phenomena (Weiss, 1981c). The biometrical paradigm asserts that continuous variation implies the determination of many genes with small effects.

"For, to date, the only popular version of hereditarianism with regard to I.Q. has been one that invokes the influence of many genes - a figure of about one hundred is sometimes mentioned . ... Why then, it might be asked, do these independent ontogenetic originators of g-differences not express themselves at all in test performances in their own right? Why do they not result indeed, in a disunitarian picture of radically independent mental abilities?" (Brand, 1984).

Although the logical contradiction seems obvious between one general factor and the assumption of many genes as its necessary neurochemical equivalent, the conclusion was not drawn either to reject the general factor or the dogma of polygenic determination of intelligence (Akesson, 1984). And nobody dared to say that a polygenic background is contradicted by obvious facts of social reality (compare Table 2). What consequences should follow from such a polygenic background in combination with an IQ correlation of 0.50 between spouses? Body height in humans runs from 1.40 m up to 2.00 m and its genetic background consists of probably several loci and an unknown number of alleles. Everyday experience shows us that despite acceleration and obvious Mendelian segregation, as a consequence of assortative marriage with regard to body height, healthy tall parents of about 1.85 m have never healthy children or grandchildren of 1.50 m or vice versa. If the genetic background for general intelligence would be similar, the rise of a rigid cast-like society would be promoted and the breeding experiment of Indian society would have had much more success. A simple genetic polymorphism prevented such a development and guaranteed the dynamics and mobility of modern society. A broad middle-class, marrying up and down and among themselves, connects the social extremes. Where inherited wealth and power tend to immobilize a society, the gifted grandson of an unskilled worker (and the author himself is one) defies such privileges, and the enlightened ruler opens the floodgates of social mobility, that means access to higher education on the basis of giftedness.

Every textbook of psychology says that intelligence scores (Guthke, 1988) are distributed normally. And about 1970 every textbook of genetics said that traits with normal distribution can only have a multifactorial and polygenic background from which the effects of single genes cannot be discerned (see Von Schilcher, 1988; Propping, 1989, for the current state of the field). Aware of this, in 1969 the author told to his mentor, Professor Grimm , that a classical genetic analysis of mathematical giftedness and intelligence would be completely impossible. A bit displeased, Grimm requested that the author should nevertheless try his best. To his surprise, the author himself was converted from polygenic to major gene theory by his own empirical findings (especially by Table 2). However, in view of the current textbook assumptions, claiming to have empirical evidence for a major gene of intelligence (Weiss, 1972), could only be a cry in the desert.

"The polygenic theory of individual variation in mental ability leads us to expect a more ore less normal distribution of ability in the population and a normal distribution of ability among siblings within the same family. Without going into the evidence for the polygenic theory of intelligence, which is now generally accepted by geneticists, I shall indicate its theoretical connection with the normal distribution of ability. The polygenic theory holds that individual variation in intelligence is the result of a number of small, similar, and independent influences that either enhance or diminish the development of a person` s intelligence" (Jensen, 1980, p. 80).

And he adds (p. 87):

"Finally, psychologists accept the idea that intelligence is normally distributed because no compelling alternative theory or evidence for any other kind of distribution has ever been proposed. ... Because this has never been done, the normal distribution of intelligence is probably the most unrivaled theory in all of psychology."

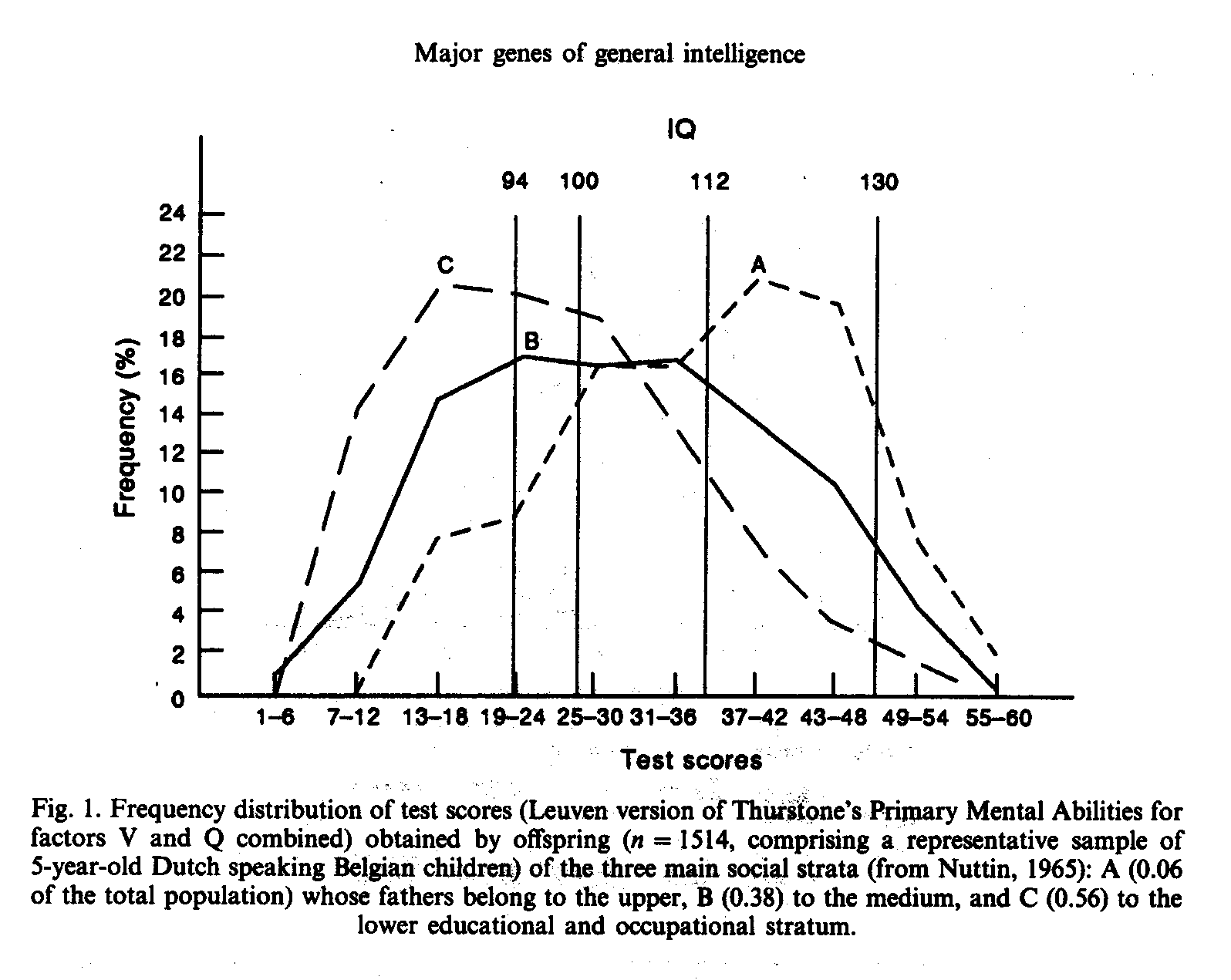
Where polygenic theory predicts a normal distribution of ability among siblings of the same family, major gene theory predicts that the IQ distribution of the offspring of homozygotes (either M1M1 or M2M2) and their spouses (much of them M1M2 in any case) should be quite markedly skewed (and the skewness should be in the opposite direction for M1M1 offspring compared to M2M2 offspring). In a representative sample (Nuttin, 1965) of Dutch speaking Belgian children (n = 1514; 5-6 years old), 6% of the fathers were classified into the upper educational and occupational level, 38% in the medium and 56% in the lower. Percentages and classifications are not identical with our (Weiss, 1982) findings, but there is a remarkable similarity. The IQ distribution of children exhibits the predicted skewness (see Fig. 1). As could be expected, also the variance of the segregating medium level is especially large. However, this argument should not be overstressed. Because of possible IQ normalization and scaling effects skewness could easily be obscured in other studies. M1M1 subjects with M1M2 spouses segregate into 50% M1M1 and 50% M1M2 and the overall M1M1 offspring can easily be clustered with near normality around a mean between IQ 130 and IQ 112 (compare Jensen, 1973, p. 171, showing the distribution of the Terman gifted offspring, in which case, considering a cut-off score of IQ 140 for one parent, a heavy regression to the mean could be expected, because according to major gene theory, IQ values above 130 have the same genetic true score as the IQ 130 itself.) The use of test raw scores instead of IQ should be more appropriate to unravel skewness, as we will show in the following.

The most convincing evidence for the major gene theory will neither come from inferences based on occupational stratification nor from psychometric data but from segregation analysis using more basic variables, for example chronometric and biochemical ones. Jensen (1980, p. 183) as a psychologist is of the opinion that "the genotype is itself a theoretical construct. No one can look at a genotype for intelligence under a microscope or isolate it in a test tube." But this is exactly for what a geneticist should strive for.

About 1970 the author (Weiss 1974), as a geneticist by training, was well aware that genotypes, who could be separated qualitatively by electrophoresis of human blood, could exhibit quantitatively a normal distribution of enzyme activitities (see Fig. 2). This finding of Harris (1966), in this case with three alleles A, B and C, was a breaktrough (compare Thoday and Thompson, 1976) and a severe blow against the arguments of biometrical genetics that for such distributions only heritabilities could be calculated, and a Mendelian analysis would be impossible. Now, in 1991, dozens of such cases of normal distributions with known underlying genotypes could be cited. (Besides, the heritability for this distribution is 0.82; Eze et al., 1974.) Harris (1966) showed that the frequency distribution curve for enzymic activity of each genotype is approximately normal and that the curves for all the genotypes add together to give a continuous unimodal distribution which is very similar to a normal distribution curve.

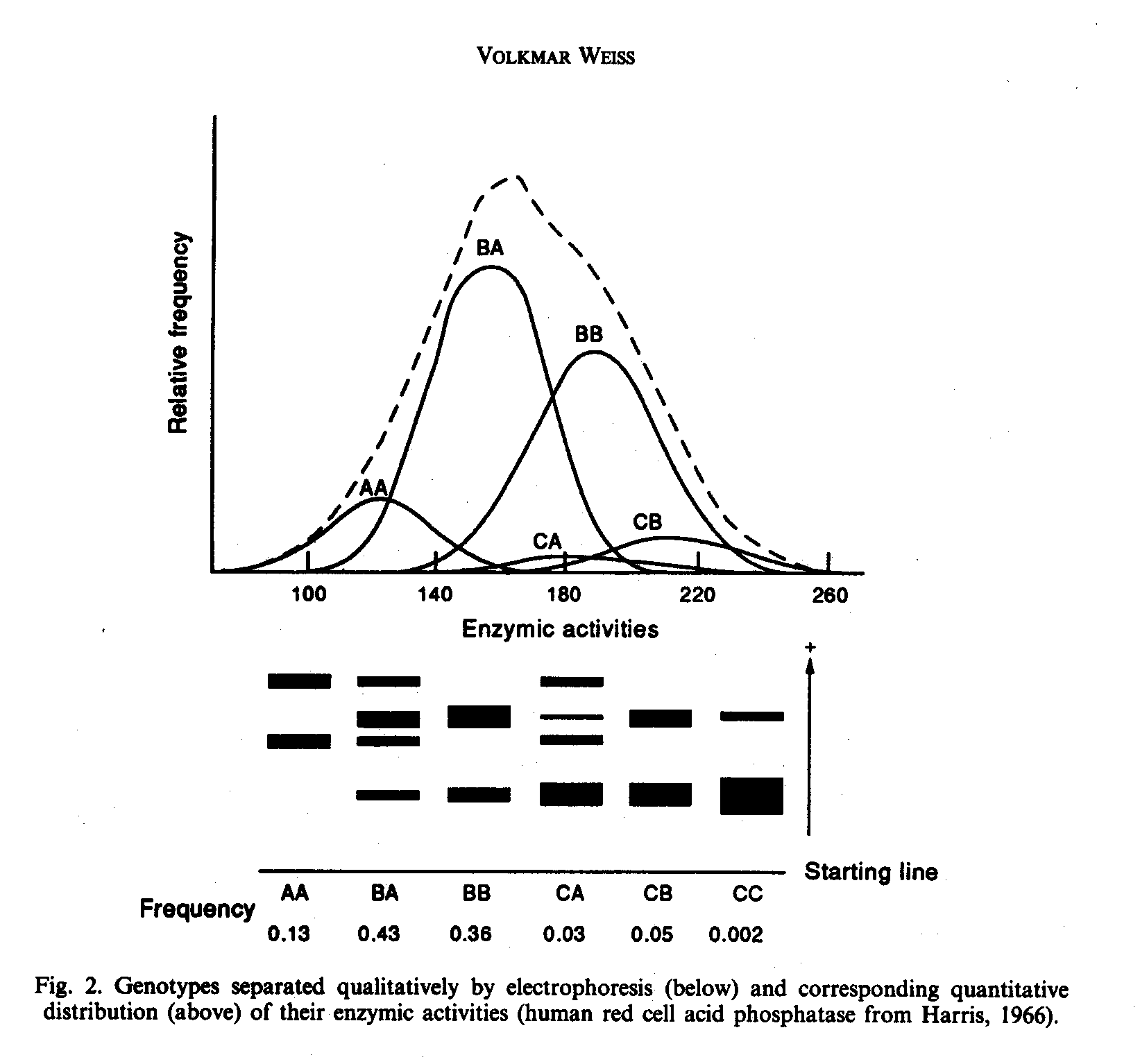
In such genetic enzyme polymorphisms the mean m2 for the heterozygotes (for example, M1M2) proved to be very often to be intermediate between the means m1 and m3 for the two homozygotes (M1M1 and M2M2).

And even more important, the standard deviations are directly proportional to the means (or si/mi, the coefficient of variation, is constant):

.

The importance of this finding (Spielman et al., 1978) cannot be stressed enough, because it reveals an underlying constant relationship between variance, speed and capacity in terms of genetics and biochemistry. Individual differences in energy transduction amd hence individual differences in capacity have their background in enzyme polymorphisms, in which different enzyme activities mean different speed of energy transmission and different variances mean different error rates of transmission. However, all three variables, speed, capacity and error, are interlinked not only by the statistical laws of biochemistry but even more and far deeper by those of statistical mechanics (see Weiss, 1986). Psychologists discussing whether individual differences in capacity, speed or error of transmission of information are more important for IQ (Eysenck, 1986, 1987; Lehrl and Fischer, 1990; Jensen, 1991) should be aware of this relationship between the three variables from the point of view of information theory and physics. Looking at IQ scores (as known always standardized to the normal curve), we cannot find any relationship between the means of M2M2 (IQ 94), of M1M2 (IQ 112) and of M1M1 (IQ 130) and their respective standard deviations. However, by looking at the test raw scores we can make a discovery (Weiss, 1979):

For all raw scores of tests of information processing speed holds the law (see Table 5) that there is a linear relationship between the means of IQ 94, of IQ 112 and of IQ 130 and their respective variances. The more intelligent, the higher the speed of information processing, the less time is needed for solving a task and the less the variance of test scores. The relationship is such a strong one that the variance of scores itself can be standardized to give a measure of IQ in such a way.

The relationship between the means is not always 2 : 3 : 4 (see Table 4). In subtest 3 of the LPS (where the subject has to choose among 8 alternatives; Horn, 1962) as in subtests of the Culture Fair Test (Cattell and Weiss, 1971) it is 4 : 5 : 6, in the subtest perceptual speed (as a pure measure of "inspection time") of the Thurstone` s Primary Mental Abilities (1963) it is 1 : 2 : 3. The latter subtest can be solved with only one glance, solving the other tests needs far more sensory input and considerable effort of sensory discrimination between the given alternatives. Therefore, we can conclude that to a constant difference in choice reaction time between M1M1, M1M2 and M2M2, we must add in some tasks a certain time amount for simple sensory discrimination, not reflecting the same basic law.

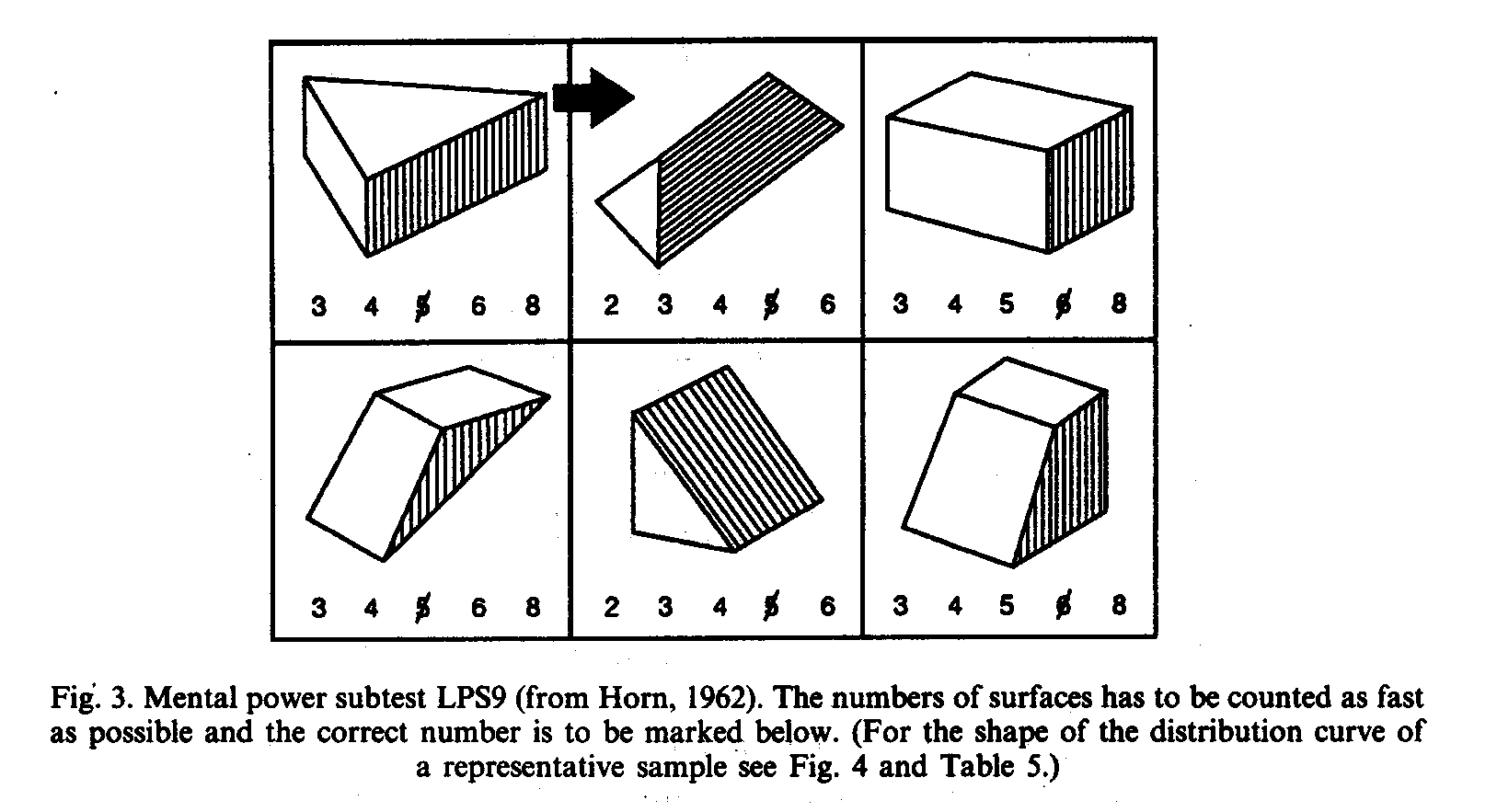
In 1989 the author, who had spend much time and effort (Weiss, 1974; see Weiss, 1982b, for a review) to propagate the fact that a normal distribution does not exclude the existence of an underlying genetic polymorphism (see Fig. 2), became aware to his amazement (Weiss, 1979) that distributions of elementary cognitive tasks were never distributed normally. Of course, under the prerequisite that each task or each selected item has nearly the same difficulty (as it is, for example, in the case of the LPS subtest 9, by Horn, 1962, see Fig. 3, where the number of surfaces has to to be counted as fast as possible; for the resulting distribution of scores see Table 5 and Fig. 4). It is not without irony, but it almost seems that IQ scores are normalized by psychologists in order to render deeper insights more difficult.

In 1978 softening of the communist ideology in East Germany (Weiss, 1991) made it possible to test a sample of 124 mathematically highly gifted youth (Weiss, 1979a) selected on the same basis as in 1970. The mean IQ of this sample was 135 plus or minus 9 (compare Table 6) corroborating in such a way the IQ estimates made on the basis of occupations (Stewart, 1947) , degree of selection and comparison with other authors (Terman, 1925). Additionally, it was possible to test another sample of 274 gifted subjects who were enrolled in special forms with extended lessons in Russian language. The distribution of this sample was clearly bimodal with one modus approx. IQ 112 (M1M2), the other approx. IQ 130 (M1M1). For the sake of comparison in Table 6 the distribution of the representative sample by Horn (1962) for children of the same age from 15 to 18 years is also given.

A difference between IQ 100 and IQ 130 suggests a difference of size, comparable to a difference of body height between a man of about 1.50 m and a man of about 1.85 m. However, this is an another illusion caused by IQ normalization. Test raw scores of elementary cognitive tasks show a skewed distribution (compare Fig. 4) in which the upper extreme of the IQ scale is about the 4-fold raw score of IQ 75 marking the threshold to the mentally retarded. Intellectually, a man with IQ 92 is a dwarf with a body height of 0.60 m standing beside a man of 1.80m and IQ 130 (compare Table 1).

Encouraged by such empirical facts, in 1982 Weiss (1982a and 1982b) published a preliminary sketch of the distribution of test raw scores for the overlapping genotypes M1M1, M1M2 and M2M2 (see Fig. 4).

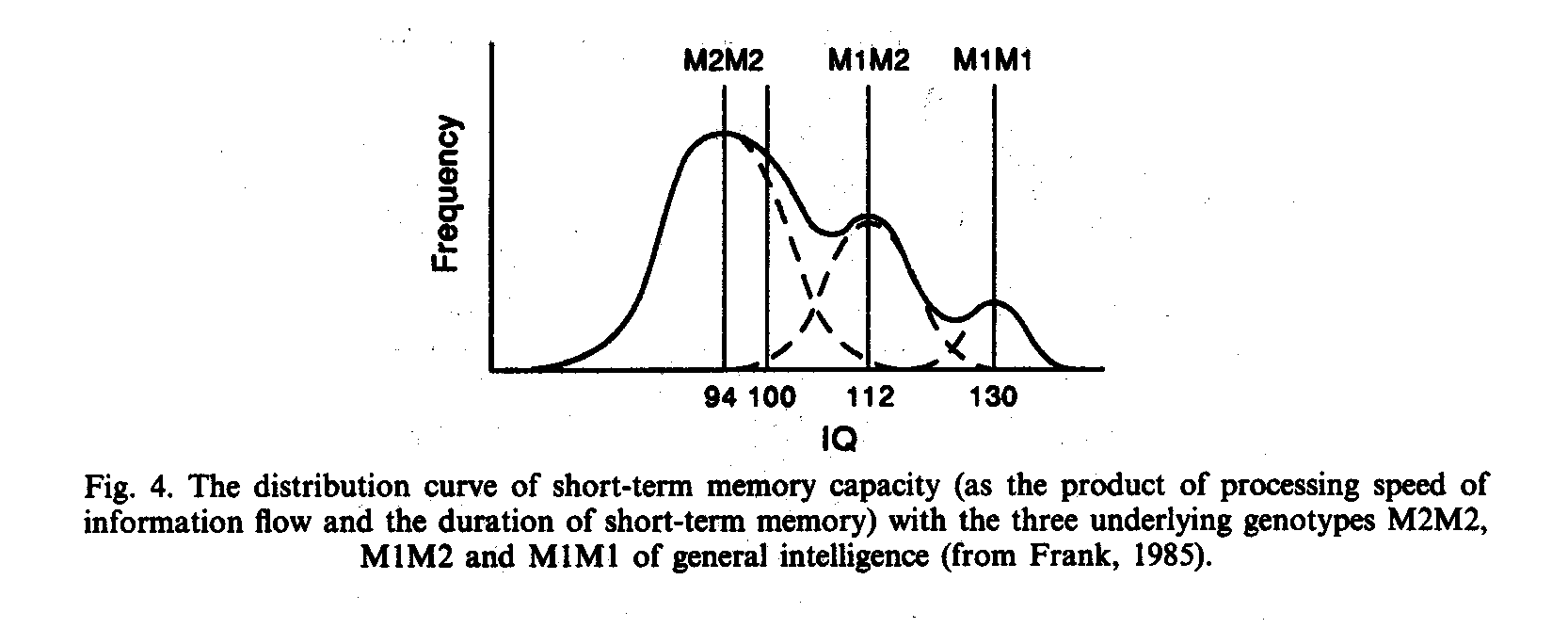
As a consequence of the relationship between speed and capacity (Spielman et. al., 1978) Weiss put forward the hypothesis that between the scores of the means of the three genotypes would always exist a linear relationship with the heterozygotes M1M2 exactly intermediate between the homozygotes, if information processing would be measured in bits, that means on an absolute physical scale. Only several weeks after the publication this hypothesis could be confirmed by Lehrl and Frank (1982).

Previously in 1959 Frank (Garfield, 1989; Lehrl and Fischer, 1990) had claimed that cognitive performance is limited by the channel capacity of short-term memory (Kyllonen and Christal, 1990). He argued that the the capacity C of short-term memory (measured in bits of information) is the product of the processing speed S of information flow (in bits per second) and the duration time D (in seconds) of information in short-term memory absent rehearsal. Hence,

see: The Basic Period of Individual Mental Speed (BIP)

According to Frank (1985) the mean of M1M1 is 140 bits, of M1M2 105 bits, and of M2M2 70 bits, that means the contribution of a single M1 allele to short-term memory storage capacity is about 70 bits, of a M2 allele about 35 bits. (For a heterozygote M1M2 hence 70 bits + 35 bits = 105 bits.)

As is well known, processing speed can in psychometric test batteries be operationalized by measuring choice reaction time or speed of mental rotation, through reading rates (Lehrl, Gallwitz and Blaha, 1980; updated by Lehrl, Gallwitz, Blaha and Fischer, 1991), scanning information in short-term memory, inspection time and time to escape masking. - The duration time of information was operationalized by memory span (Lehrl, Gallwitz and Blaha, 1980), a phenomomenon which plays a crucial role in psychological theory since about a century. For example, Pascual-Leone (1970) in his pioneering empirical research understood memory span as the maximum of discrete indistinguishable energy units which every subject has at his disposal. NeoPiagetian theorists have claimed memory span to be the missing link between psychometrically defined intelligence and cognition, i.e. span to be the most important human limitation in reasoning and problem solving. According to Lehrl, Gallwitz and Blaha (1980), the forward digit span of M1M1 subjects should have a mean between 8 and 9, of M1M2 of about 7, of M2M2 of about 6. It is pity, however, that the theoretical importance and the test reliability of this span phenomenon are inversely correlated (and 7 should always be read with the addition plus or minus 2; Miller 1956).

Weiss, who was not aware of the importance of memory span before he became acquainted with Frank` s theory (Lehrl and Frank, 1982), in the following years in a series of papers (Weiss, 1986, 1987, 1989, 1990a; and under the pseudonym Weisman, 1988) was able to show correlations between IQ and memory span on the one hand and the EEG power spectral density on the other. In statistical mechanics he could find the theoretical explanation (Weiss, 1989 and 1990a) why memory span is identical with the number of zero-crossings of event-related potentials of the EEG between the onset of conscious information processing of a stimulus and the P300. Because an evoked response of the EEG can be understood as the impulse response of a certain individual, dependent upon the respective mobilization of energy as the critical factor in producing the wave form, again the importance of individual difference in brain energy metabolism for IQ is stressed. Here is not the place to go into details and the interested reader should consult the original series of papers, published by Weiss since 1986.

Although the human brain represents only about 2% of the body weight, its energy consumption is about 20% of total body energy requirements. The brain consumes glucose as an almost exclusive source of energy (Mac Candless, 1986). It would defy the most fundamental laws of thermodynamics, if individual differences in general mental power would not find their counterpart in individual differences in cerebral energy metabolism. According to thermodynamics, the measurement of 1 bit of information requires a minimum energy of 1 kT x ln2 (Szilard, 1929), where k is Boltzmann` s constant and T is absolute temperature. Therefore, it is an outstanding event that three independent research groups (De Leon et al., 1983; Chase et. al., 1984; Riege et al., 1985) reported significant correlations (mean around 0.60) between cerebral glucose metabolism rate and a number of IQ tests, including the subtests memory span and mental speed, in both the Alzheimers patients and healthy control groups separately. Alone De Leon et al. (1983) reported 141 significant correlations; Riege et al. (1985) 38 correlations. Of course, this does not mean that high IQ subjects for accomplishing a given task or test item need more metabolic fuel than low IQ subjects (see Haier et. al., 1988, for the empirical confirmation of this relationship.) This would be a clear disadvantage. At the contrary, "floating" brains of high IQ subjects think more ahead per unit time than low IQ subjects and therefore need at an average more energy per unit time. Positive correlations between glucose metabolism rate and IQ were found when this rate and IQ were measured separately, a negative correlation (Haier et. al., 1988) when the subjects did a test during the uptake of the glucose.

When a high correlation between IQ and a psychophysiological, electrophysiological (Chalke and Ertl, 1965) or biochemical variable (such as glucose metabolism rate) has been found by a research group, 20 years later there will always be as much confirmations and non-confirmations of the original finding. It is one of the striking properties of an underlying major gene locus of general intelligence to provide an explanation why so many results have never been replicated or only with unsatisfying low correlations (Weiss, 1982c). If we sample only within the range of one genotype, e.g., the sample comprises only university students of mathematics and physics (all M1M1), then all correlations between the various subtests of IQ, mental speed, memory span or average evoked potentials of EEG and biochemical parameters tend to become zero (even heritabilities tend toward zero). The small remaining correlations are mostly the correlations of error scores in a broader sense (Weiss, 1979b) and nothing else. The same applies if a sample includes only healthy probands with IQ in a range below 104. If the sample is of subjects representing the genotypes in equal proportions, the empirical correlations will reach their maxima (up to 0.8). And consequently (and because the gene frequency of M1 is 0.2 and not 0.5), for a sample representative of the whole population the correlations will be lower again (about 0.4). Look at the descriptions of the samples replicating or rejecting correlations with IQ, and it will be a true revelation! A statistical meta-analysis of all such studies is urgently needed. Until now, there is too little understanding of this statistical problem (see, for example, Juhel, 1991) which cannot be accounted for by mere attenuation for restriction of range. Consequently, one cannot assert that some research groups have intentionnaly planned their study in such a way that nonconfirmation could be the only result (Weiss, 1991). Unintentionally, for example, Vogel et al. (1987) have fallen into this methodological trap with an above-average IQ sample, only mostly M1M2. However, if this is understood, you can ever and always devise a research methodology which rejects any correlations with IQ. That factor analytic studies of intelligence with the always underlying assumption of a continuum of many small effects (and genes) could never come to a consistent result, beside the existence of a general factor (if the sample was fairly representative), is also a consequence of the threshold properties of major genes.

Major genes of intelligence have so many implications that it is difficult to imagine that 90 years of research should have not brought about empirical results which gave hints to the existence of such genes (Akesson, 1984). For example, Terman in his sample of gifted could not find (Terman and Oden, 1948) any significant differences in later achievements between IQ 170 and more and an IQ of approx. 140. "Those with IQs of 196 (the highest) did not earn more than those with IQs of 135 (the lowest)," confirms Ceci (1990) claiming this would support his argument "that IQ has little relationship to real-world attainments". However, this is exactly what should follow from major genes, where beyond IQ 130 all individuals should be M1M1.

The logic of this argument can be extended: In a three-generation study (compare Warner and Abegglen, 1955) the test scores of children of gifted M1M1 probands should be independent from the scores of the gifted probands themselves and only dependent upon scores of their spouses (i.e., whether they are M1M1 or M1M2). We are planning a similar second follow-up study with our mathematically gifted probands, who have their own families in the meantime. In this follow-up study it will be easier to test IQ and to replicate Mendelian segregation in the families of the sibs of probands, that means among their nieces and nephews instead of cousins (see Table 2). Whoever wants to replicate or to disprove the results of Table 2 will easily find in any developed country 200 mathematicians and physicists (all M1M1 per definition), whose collaterals he can test.

Major gene theory always predicts a certain distribution and segregation. A general review will find dozens of studies and distributions of past studies with IQ tests far from normal. However, because there was no alternative theory of IQ, chance or lacking representativity was the only answer, preventing any deeper critical insight. An especially striking example is Herrnstein` s (1973) interpretation of the World War II Army General Classification Test published by Stewart (1947): "The average values of the single occupations are dispersed from 129 to 85, and inbetween we see the wellknown bellshaped distribution curve" (see Fig. 5). I see a bimodal distribution with the modi about IQ 94 (M2M2) and IQ 112 (M1M2). Near the IQ 100 modus of a normal distribution about 6000 probands are lacking. (A M1M1 modus around IQ 130 was impossible, because officers were not tested.)

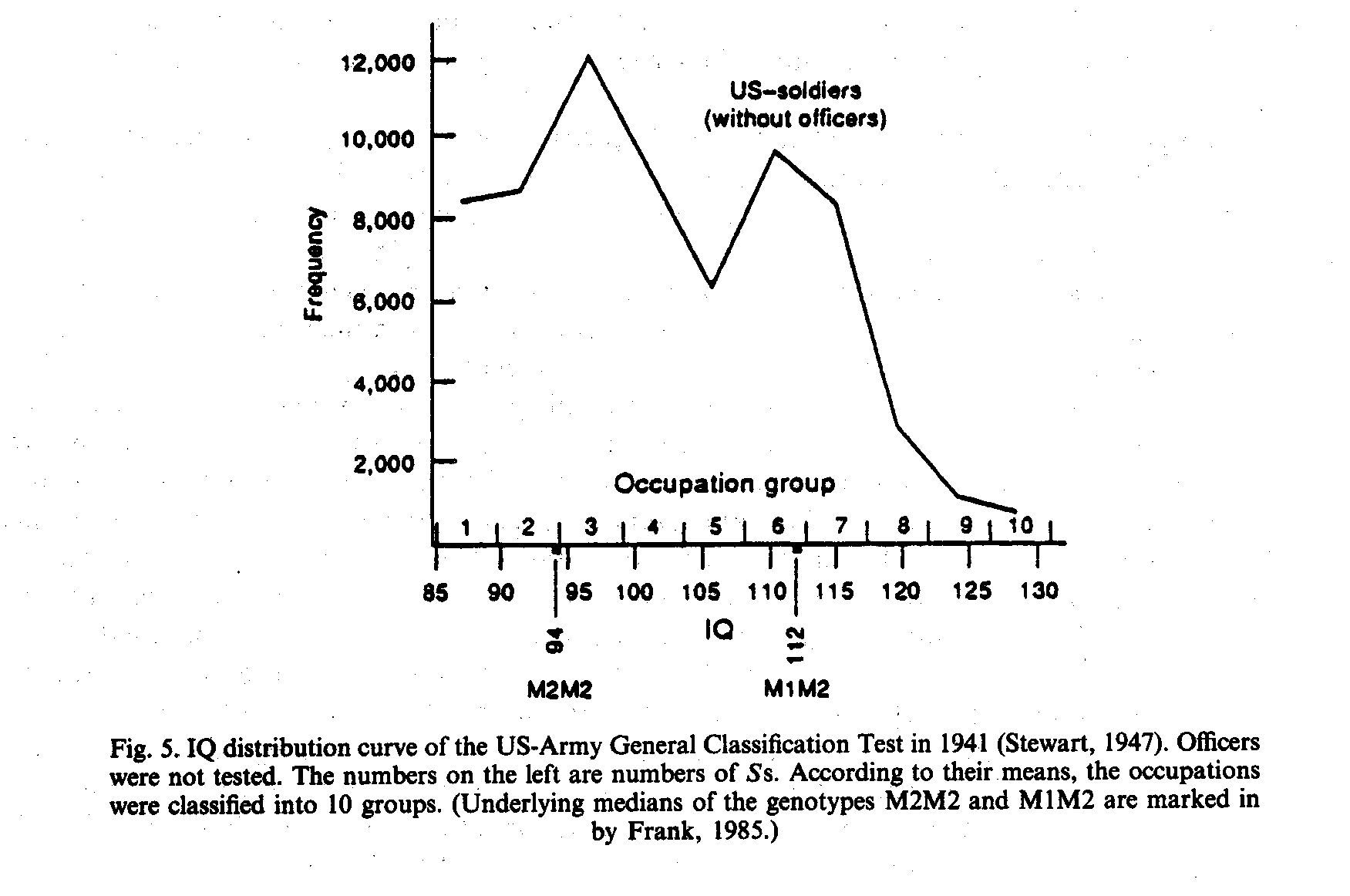Was there never a Mendelian approach? In 1915 Peters (for his biography see Weiss, 1980) had published a study, sponsored by the Imperial Academy of Science in Wien and comprising 344 parental pairs with 1162 children and 151 complete data sets from all four grandparents. The sample was drawn form villages in Southern Germany and Austria. Because IQ tests were impossible, only school marks were available (compare Table 7).

Full aware of the high unreliability of marks, nevertheless, Peters drew the conclusion that parents with mark 1 should be a mixture of homozygous and heterozygous (M1M1 and M1M2 in our terminology) individuals, such with mark 3 only homozygous (M2M2). To his surprise, under the assumption of overlapping distributions the data fitted simple Mendelian segregation very well. However, the study remained without any response. Also in Germany correlation statistics and normal distribution became for about 50 years the only permitted way of analysis of IQ (Weiss, 1982b).

There are professions, such as bankmanager or physician, where both social tradition of the family and intellectual endowment play an important role. For example, in Wales (Mc Guffin and Huckle, 1990; n = 249)

"the overall percentage of first degree relatives attending medical school was 13.4%, compared with approximately 0.22% of the general population. ... It is probable that genetic factors do contribute to the familiarity of attending medical school; but the major-gene hypothesis is, on commonsense grounds, highly implausible. It is far more likely that the major source of family resemblance for this trait derives from family culture and shared environment than from shared genes. ... However, the recessive-gene hypothesis withstood the test, and thus far our analysis, using modern, more sophisticated methods, replicated findings published more than 30 years ago" by Lilienfield (1959).

And despite their commonsense prejudice, McGuffin and Huckle cannot withhold to state: "We have more consistent, and somewhat more persuasive, evidence of a major gene for attending medical school than for any of the neuropsychiatric disorders." Of course, there is no major gene for attending medical school but for underlying general intelligence.

Metabolically the usual mathematical notion of small and additive effects of many genes for polygenic inheritance is violated by the hierarchical nature of biochemical conversions in the human brain (Mac Candless, 1986). Certain enzyme-catalyzed reactions are rate-limiting for a pathway or are involved in more essential pathways than others. If appreciable variability of a trait is due to Mendelian segregation at a single locus we speak of the major gene locus of that trait. In a statistical analysis a major gene can only be traceable, if there is a biochemical reality, a gene that can be discovered. To prove the existence of the major gene locus of human intelligence will be a discovery of centennial importance, and therefore it is for the one science fiction, for the other a nightmare (Weiss, 1991), but it will be in every case an intellectual shock.

But the future has already begun. Since the existence of a major gene locus had some probability (Weiss, 1972), it was the declaired aim of the author to find ways and means to promote the discovery of the underlying enzyme polymorphism. What was known about this polymorphism: Since 1971 (Weiss, 1972, 1973) its gene frequency and its strong correlation with social status; since 1979 (Weiss, 1979) its distribution properties; since 1982 (Lehrl and Fischer, 1982) its probable involvement with brain energy metabolism (see Weiss, 1987).

More than a decade long the author was browsing the entire literature on genetic polymorphisms and any correlations between IQ, social status and physical variables without finding any end of a logical thread. Polymorphisms with gene frequencies about 0.20 are not uncommon, and all such hints led only into dead alleys. A number of already known polymorphisms in brain metabolism are not correlated with IQ and social status and this missing correlation told that the trail was false again.

In 1982 I became aware (Weiss, 1982a) of a paper published by Sinet, Lejeune and Jerome (1979) in which a correlation of 0.58 between IQ and erythrocyte glutathione peroxidase activity (GSHPx) was reported for 50 trisomy 21 patients. None of the other enzymes studies correlated with IQ. The IQ of controls had not been tested by Sinet, Lejeune and Jerome because they thought the correlation to be trisomy-specific. However, Fraser and Sadovnick (1976) had found that the correlations of IQ between trisomy 21 probands with their fathers, mothers and sibs are about 0.50, consequently of the same size as with healthy children despite the mean IQ of trisomy 21 probands is about 70 points lower. Therefore Lenz (1978) concluded individual differences in trisomy-IQ have the same biochemical background as in normal persons. - In population studies a mean enzyme activity of about 24 U GSHPx/g Hb was found. In contrast 100 healthy university students had a mean of 40.5 U, what seems to be another argument for the association of high IQ with high GSHPx activity (for more details and references see Weiss, 1984 and 1987).

Also glutathione S-transferases (GST) possess GSH peroxidase properties. Until now, there are no data on whether the correlation between IQ and GSHPx is the mixed result of GSHPx and GST activities, or is only the effect of either GSHPx or GST. In 1985 Seidegard and Pero discovered a polymorphism of GST whose gene frequencies and distribution properties are completely identical with the wanted major gene locus of intelligence. The polymorphism turned out to be a polymorphism of GST1 (Seidegard, Pero and Stille, 1989). However, until now nobody has ever measured the correlation between GST1 (ligandin) activity and IQ.

Another enzyme claimed to be involved in signal transduction and memory formation by many authors (see for a review, Nishizuka, 1989) is protein kinase C 1. In 1989 Taniguchi and Pyerin published a paper in which GST was found to be a substrate of protein kinase C. From 6 isozymes of GST purified from liver cytosol only GST1 was phosphorylated by the kinase (compare also Sakai, Okuda and Muramato, 1989) purified from brain. In a letter of January 4, 1990, Seidegard wrote to the author: "The paper by Taniguchi and Pyerin might open a new research front. ... However, sometimes it is very difficult to keep in mind the differences of nomenclature of GST in different species as well as as between different research groups." Because not only GST but also protein kinase C have turned out to be enzyme families of high molecular heterogeneity with different tissue specifities (Carder et. al., 1990), an easy answer will not be found.

Some essential pieces of the biochemical puzzle are still lacking. The cited correlations were always found as mere byproducts of medical research. In all cases the physicians were not aware of the possible implications of their findings amd mostly deeply frightened to be accused of "reactionary science" (compare Weiss, 1991), when they became aware of interpretations (Weiss, 1984, 1987) of their work. As a rule, all further empirical work in the given direction was stopped by a mechanism of self-censorship.

At present, two ways can be imagined for the prenatal determination of the IQ of a foetus: electrophysiological (Hepper,1989) or biochemical measurement. Whether there it will be necessary to culture cells in order to multiply fetal tissue from biopsy or whether microanalysis will be so sensitive that the immediate biochemical determination of genotypes and hence of IQ-range will be possible, future will tell us.

The most impressive fact of racial differences in intelligence is their smallness (Lynn, 1991). Differences between social strata within one population are larger than between races. We all know that an occupational group with higher education, whether black, white or yellow, has a mean IQ of about 30 points higher than the social stratum of unskilled workers.

Despite many thousand years of relatively independent evolution, Mongoloids in East Asia and Caucasoids in Europe (and in the New World) appear to have similar gene frequencies of general intelligence. A major gene theory with an allele frequency of about 0.20 for a gene M1 responsible in the homozygous state for an IQ of 130 (Hagemann, 1988) is in accordance with the facts of social mobility within developed societies. The crucial question is, what are the evolutionary forces which have stabilised and are still balancing (Weiss, 1990b) such a frequency of about 5% high IQ individuals and about 27% heterozygous individuals and hence a general population mean of about the same level in Mongoloids and Caucasoids? In developed societies high intelligence of a person seems to be of such an advantage, that one wonders why the major gene M2 responsible for lower normal intelligence has survived with a frequency of about 0.80.

A relatively stable social hierarchy needs a small number of high IQ individuals at the top, a greater number of individuals of average intelligence for the middle positions, and a large number of low IQ individuals to perform modest routine work at the bottom. In modern societies M1M1 individuals invent machines, M1M2 repair machines, and M2M2 operate machines. Any hierarchical society can only tolerate a very small percentage of high IQ individuals in relatively humble social positions, because such individuals represent always, in view of the limited number of leading positions, a potential threat to the ruling elite. In economically dynamic societies there is always periodic turbulence, and the antagonism between ruling and powerless high IQ-individuals, i.e. the struggle for leadership of the majority, is the most potentially destabilizing factor, not the direct challenge to the ruling elite by the low IQ majority itself. All societies have to have a hierarchy with a relatively fixed ratio of leading to nonleading positions.

During the ice ages somewhere in Eurasia there arose the superior M1-mutant. This mutant must have conferred a selection advantage and spread. (It appears that this mutation was never introduced into the Australian aborigines before 1750.) A pack of mammoth hunters of about a dozen men with an IQ of 94 and half a dozen heterozygotes with an IQ of 112, led by an alpha male with an IQ of 130 became an optimal foraging unit. Such a one-level hierarchy, based on a division of labour correlated with intelligence, was the prerequisite for the rise of multi-level societies. However, this rise was not accompanied by a fundamental change of the stabilizing forces of the genetic polymorphism itself. It seems that multilevel hierarchies in Europe and East Asia were very reluctant and unsuccessful in creating for gifted surplus offspring additional niches where survival could be correlated with reproductive success above average.

Footnote (1)
The frequency (in percent) with which a gene combination manifests itself in the phenotype of the carriers.
Penetrance (as well as expressivity) depends both on the genotype and the environment. Penetrance is complete when all the homozygous recessives show one phenotype and when all of the heterozygotes are alike. If less than 100% of the carriers of a certain genotype manifest that phenotype characteristic for the class, penetrance is reduced or incomplete. Penetrance of a gene may be identical or different in sex, or in extreme cases, may be limited to one or the other sex" (Rieger, Michaelis & Green, 1976).

Note added in proof

For tracing the biochemical background of IQ, the newly discovered link between gluthathione status and the NMDA receptor (Sucher & Lipton, 1991) could be very important.

ACKNOWLEDGEMENT

I would like to thank Prof. A. R. Jensen (Los Angeles) for his constructive comments on the first draft of this paper.

• Akesson H. O. (1984) Intelligence and polygenic inheritance. A dogma to re-examine. Acta Paediatr. Scand. 73, 13-17.

• Brand, C. R. (1984) Intelligence and inspection time: an ontogenetic relationship? In The Biology of Human Intelligence (Edited by Turner C. J. and Miles H. B.). Nafferton, Nafferton Books.

• Carder P. J., Hume R., Fryer A. A., Strange R. C., Lauder J. and Bell J. E. (1990) Glutathione S-transferase in human brain. Neuropathol. Appl. Neurobiol. 16, 293-304.

• Cattell R. B. and Weiss R. H. (1971) Grundintelligenztest CFT 3 - Skala 3. Westermann, Braunschweig.

• Ceci, S. J. (1990) On the relation between microlevel processing efficiency and macrolevel measures of intelligence: Some arguments against current reductionism. Intelligence 14, 141-150.

• Chalke F. and Ertl J. (1965) Evoked potentials and intelligence. Life Sciences 4, 1319-1322.

• Chase T. N., Fedio P., Foster N. L., Brooks R., Di Chiro G. and L. Mansi (1984) Wechsler adult intelligence scale performance: cortical localization by fluorodeoxyglucose F 18-positron emission tomography. Arch. Neurol. 41, 1244-1247.

• Crow, T. J. (1991) A single locus for psychosis and intelligence in the exchange region of the sex chromosomes? In Ethical Issues of Molecular Genetics in Psychiatry (Edited by Sram R. J., Bulyzhenkov V., Prilipko L., and Christen Y.), pp. 12-33. Springer, Berlin.

• De Leon M. J., Ferris S. H., George A. E., Christman D. R., Fowler J. S., Gentes C., Reisberg B., Gee B., Emmerich M., Yonekura Y., Brodie J., Kricheff I. I. and Wolf A. P. (1983) Positron emission tomographic studies of aging and Alzheimer disease. Am. J. Neuroradiol. 4, 658-571.

• Engel W., Pirl U. and Titze H. (1971) Die Olympiaden Junger Mathematiker in der Deutschen Demokratischen Republik - ihre Entwicklung bis zum Jahre 1971. Mitt. Math. Ges. DDR No. 2, 5-39.

• Eysenck H. J. (1986) The theory of intelligence and the psychophysiology of cognition. In Advances in the Psychology of Human Intelligence (Edited by Sternberg R. J.), Vol. 3, pp. 1-34. Erlbaum, Hillsdale, N.J..

• Eysenck H. J. (1987) Speed of information processing, reaction time, and the theory of intelligence. In Speed of Information-Processing and Intelligence (Edited by Vernon P. A.), pp. 21-67. Ablex, Norwood.

• Eze L. C., Tweedie M. C. K., Bullen M. F., Wren P. J. J. and Evans D. A. P. (1974) Quantitative genetics of human red cell acid phosphatase. Ann. Hum. Genet. 37, 333-340.

• Frank H. (1985) Is intelligence measurable and is it inherited? Folia human. 23, 671-691.

• Fraser F. C. and Sadovnick A. D. (1976) Correlation of IQ in subjects with Down syndrome and their parents and sibs. J. Ment. Defic. Res. 29, 179-182.

• Garfield E. (1989) More delayed recognition. Part 1. Examples from the genetics of color blindness, the entropy of short-term memory, phosphoinositides, and polymer rheology. Current Contents 21, No. 38: Current Comments 3-8.

• Garrison R. J., Anderson V. E. and S. C. Reed (1968) Assortative marriage. Eug. Quart. 15, 113-127.

• Gille R., Henry L., Tabah L., Sutter J., Bergues H., Girard A. and Bastide A. (1954) Le niveau intellectuel des enfants d` age scolaire. La determination des aptitudes. L` influence des facteurs constitutionelles, familiaux et sociaux. Cahiers de "Travaux et documents de l` Institute National d` ' Etudes Demographiques", No. 23, Paris.

• Gottfredson L. A. (1986) Societal consequences of the g factor in employment. J. Vocational Behav. 29, 379-401.

• Grimm H. (1943) Zur Erbbiologie der mathematischen Begabung. Erbarzt 11, 37-42.

• Guthke J. (1988) Intelligenzdiagnostik. In Psychologische Diagnostik (Edited by Jäger R. S.), pp. 333-347. Psychologie Verlags Union, München.

• Haenschke B. (1985) Persönlichkeitseigenschaften und Entwicklungsbedingungen begabter junger Mathematiker. Diss. B., Humboldt-Universität, Berlin.

• Hagemann R. (1988) Der Beitrag der Zwillingsforschung zur Analyse der genetischen Grundlagen der Intelligenzleistungen des Menschen. In: Vom Gen zum Verhalten (Edited by Geissler E. and Hörz H.), pp. 33-52. Akademie- Verlag, Berlin.

• Haier R. J., Siegel B. V., Nuechterlein K. H., Hazlett E., Wu J. C., Paek J., Browning H. L. and Buchsbaum M. S. (1988) Cortical glucose metabolic rate correlates of abstract reasoning and attention studied with positron emission tomography. Intelligence 12, 199-217.

• Harris H. (1966) Enzyme polymorphisms in man. Proc. Roy. Soc. B 164, 298-310.

• Hepper P. G. (1989) Fetal learning - implications for psychiatry. Brit. J. Psychiat. 135, 289-293.

• Herrnstein R. J. (1973) IQ in the Meritocracy. Atlantic Monthly Press, Boston.

• Horn W. (1962) Leistungsprüfsystem (LPS). Hogrefe, Göttingen.

• Howard-Peebles P. N. and Stoddard G. R. (1979) X-linked mental retardation with macroorchidism and marker X chromosome. Hum. Genet. 50, 247-251,

• Husén T. (1951) The influence of schooling upon IQ. Theoria 17, 61-88.

• Jensen A. R. (1973) Educability and Group Differences. Methuen, London.

• Jensen A. R. (1980) Bias in Mental Testing. Methuen, London. Jensen A. R. (1991) Spearman` s g: links between psychometrics and biology. Preprint.

• Juda A. (1953) Höchstbegabung. Urban und Schwarzenberg, München.

• Juhel J. (1991) Relationships between psychometric intelligence and information-processing speed indexes. Cahiers de Psychologie Cognitive 11, 73-105.

• Karzmark P., Heaton R. K., Grant I. and Matthews C. G. (1985) Use of demographic variables to predict full scale IQ: a replication and extension. J. Clin. Exper. Neuropsychol. 7, 412-420.

• Kyllonen P. C. and Christal R.. E. (1990) Reasoning ability is (little more than) working memory capacity. Intelligence 14, 389-433.

• Lehrl S. and Fischer B. (1990) A basic information psychological parameter (BIP) for the reconstruction of concepts of intelligence. Eur. J. Personality 4, 259-286. - see: The Basic Period of Individual Mental Speed (BIP)
  

• Lehrl S. and Frank H. G. (1982) Zur humangenetischen Erklärung der Kurz- speicherkapazität als der zentralen individuellen Determinante von Spearmans Generalfaktor der Intelligenz. Grundlagenstud. Kybern. Geistes- wiss./Humankybern. 23, 177-187.

• Lehrl S., Gallwitz A. and Blaha L. (1980) Kurztest für Allgemeine Intelligenz KAI, Handanweisung. Vless, Vaterstetten-München.

• Lehrl S., Gallwitz A., Blaha L. and Fischer B. (1991) Geistige Leistungsfähigkeit. Theorie und Messung der biologischen Intelligenz mit dem Kurztest KAI. Vless, Ebersberg.

• Lenz W. (1978) Humangenetik in Psychologie und Psychiatrie. Quelle und Meyer, Heidelberg.

• Li C. C. and Sacks L. (1954) The derivation of joint distribution and correlation between relatives by the use of stochastic matrices. Biometrics 10, 347-360.

• Lilienfield A. M (1959) A methodological problem in testing a recessive gene hypothesis. Am. J. Public Health 49, 199-204.

• Lynn R. (1991) Race differences in intelligence: a global perspective. Mankind Quart. 31, 255-296.

• Maas F. (1916) Über die Herkunftsbedingungen der geistigen Führer. Arch. f. Sozialwiss. u. Sozialpol. 41, 144-186.

• Mac Candless D. W. (Ed.) Cerebral Energy Metabolism and Metabolic Encephalo- pathy. Plenum, New York.

• McCall R. M. (1977) Childhood IQ` s as predictor of adult educational and occupational status. Science 197, 482-483.

• McGuffin P. and Huckle P. (1990) Simulation of Mendelism revisited: the recessive gene for attending medical school. Am. J. Hum. Genet. 46, 954-959.

• Miller G. A. (1956) The magical number seven, plus or minus two: some limits on our capacity for processing information. Psychol. Rev. 63, 81-97.

• Nishizuka Y. (1989) The family of protein kinase C for signal transduction. J. Am. Med. Ass. 262, 1826-1833.

• Nuttin J. (1965) De verstandelijke begaafdheid van de jeugd in de verschillende sociale klassen en woonplaatsen. Mededel. Kon. Vlaamse Akad. Kl. Lett. 27: No. 7.

• Oden M. H. (1968) The fullfillment of promise: 40-year follow up of the Terman gifted group. Genet. Psychol. Monogr. 77, 3-93.

• Pascual-Leone J. (1970) A mathematical model for the transition in Piaget` s developmental stages. Acta Psychol. 32, 301-345.

• Peters W. (1915) Über Vererbung psychischer Fähigkeiten. Fortschr. Psychol. 3, 185-382.

• Pollmer K. (1989) Zur Bedeutung von Fähigkeiten, Motiven und Interessen für Leistungserfolg von Spezialschülern mathematisch-naturwissenschaftlich- technischer Richtung. - Ein Beitrag zur Hochbegabungsforschung. Diss. B, Wilhelm-Pieck-Universität, Rostock.

• Propping P. (1989) Psychiatrische Genetik. Springer, Berlin.

• Riege W. H., Metter E. J., Kuhl D. E. and Phelps M. E.: Brain glucose metabolism and memory functions. Age decrease in factor scores. J. Gerontol. 40, 459-467.

• Rieger R., Michaelis A. and Green M. M. (1976) Glossary of genetics and cytogenetics. Jena: Fischer.

• Rossmann J. (1930) Heredity and invention. J. Hered. 21, 507-512.

• Rüdin E. (1951) Lebensbewährung, Gesundheitsverhältnisse und Herkunft einer bestimmten Gruppe von Einser-Abiturienten und ihrer Verwandtschaft. Z. menschl. Vererb.- u. Konsti.-lehre 30, 166-211.

• Sakai M., Okuda A. and Muramato M. (1988) Multiple regulatory elements and phorbol 12-tetradecanoate 13-acetate responsiveness of the rat placental glutathione transferase gene. Proc. Natl. Acad. Sci. US 85, 9546-9560.

• Seidegard J. and Pero R. W. (1985) The hereditary transmission of high glutathione transferase activity towards trans-stilbene oxide in human mononuclear leukocytes. Hum. Genet. 69, 66-68.

• Seidegard J., Pero R. W. and Stille B. (1989) Identification of the trans- stilbene oxide-active glutathione transferase in human mononuclear leukocytes and in liver as GST1. Biochem. Genet. 27, 253-261.

• Sinet P.-M., Lejeune J. and Jerome H. (1979) Trisomy 21 (Down` s syndrome), glutathione peroxidase, hexose monosphate shunt and I.Q. Life Sciences 24, 29-33.

• Spearman C. (1904) "General intelligence", objectively determined and measured. Amer. J. Psychol. 15, 201-293.

• Spielman R. S., Harris H., Mellmann W. J. and Gershowitz H. (1978) Dissection of a continuous distribution: red cell galactokinase activity in blacks. Am. J. Hum. Genet. 30, 237-248.

• Stafford R. E. (1972) Hereditary and environmental components of quantitative reasoning. Rev. Educ. Res. 42, 183-201.

• Stewart N. (1947) A. G. C. T. scores of army personnel grouped by occupation. Occupations 26, 5-41.

• Sucher, N. J. and Lipton, S. A. (1991). Redox modulatory site of the NMDA receptor-channel complex-regulation by oxidized glutathione. Journal of Neuroscience Research, 30, 582-590.

• Szilard L. (1929) Über die Entropieverminderung in einem thermodynamischen System bei Eingriff intelligenter Wesen. Z. Physik 53, 840-856.

• Taniguchi H. and Pyerin W. (1989) Glutathione S-transferase is an in vitro substrate of Ca++-phospholipid-dependent protein kinase (protein kinase C). Biochem. Biophys. Res. Commun. 162, 903-907.

• Terman L. M. (1925) Genetic Studies of Genius. Vol. I. Mental an Physical Traits of a Thousand Gifted Children. Stanford University Press, Stanford.

• Terman L. M. and Oden M. H. (1948) Genetic Studies of Genius. Vol. IV. The Gifted Child Grows up: Twenty Fife Years` Follow-up of Superior Group. Stanford University Press, Stanford.

• Thoday J. M. and Thompson J. N., jr. (1976) The number of segregating genes implied by continuous variation. Genetica 46, 335-344.

• Thurstone T. G. (1963) Primary mental abilities (PMA) for grades 2 - 4. Science Research Associates, Chicago.

• Visher S. S. (1948) Environmental backgrounds of leading American scientists. Amer. Sociol. Rev. 13, 65-72.

• Vogel F., Kruger J., Schalt E., Schnobel R. and Hassling L. (1987) No consistent relationships between oscillations and latencies of visual and auditory evoked EEG potentials and measures of mental performance. Human Neurobiology 6, 173-182.

• Von Schilcher F. (1988) Vererbung des Verhaltens. Thieme, Stuttgart.

• Warner W. L. and Abegglen J. C. (1955) Occupation mobility in American Business and Industry. University of Minnesota Press, Minneapolis.

• Weisman H. S. (1988) Toward a quantum mechanics of intelligence. In Essays on the Nature of Intelligence and the Analysis of Racial Differences in the Performance of IQ Tests (Edited by Jamieson J. W.), pp. 25-49. Cliveden, Washington.

• Weiss V. (1972) Empirische Untersuchung zu einer Hypothese über den autosomal-rezessiven Erbgang der mathematisch-technischen Begabung. Biol. Zbl. 91, 429-535.

• Weiss V. (1973) Die Prüfung von Hypothesen bei den synchron zum Probanden lebenden Seitenverwandten als Methode der Humangenetik. Biom. Z. 15, 259- 270.

• Weiss V. (1974) Ein Algorithmus für die Mendelanalyse quantitativer Merkmale. Biol. Zbl. 93, 311-323.

• Weiss V. (1978) Diskretheit der genetischen Information, aber Kontinuität der Meßwerte - zentrales erkenntnistheoretisches Problem in den Auseinandersetzungen zwischen biometrischer und mendelistischer Genetik. In: Philosphie und Naturwissenschaften in Vergangenheit und Gegenwart. No. 12: Philosophie und Biowissenschaften in der Geschichte, pp. 62-68. Humboldt-Universität, Berlin.

• Weiss V. (1979a) The physiological equivalent of the major gene locus of general intelligence: Discrete interindividual differences in central processing time of information. Acta biol. med. germ. 38, No. 1, K1-K4.

• Weiss V. (1979b) The heritability of difference scores when environments are correlated. Biometrical J. 21, 171-177.

• Weiss V. (1979c) The use of heritabilities of anthropometric measures and performance tests in personnel selection. Mankind Quarterly 19, 221-224.

• Weiss V. (1980) Zum Gedenken an den 100. Geburtstag des Psychologen und Genetikers Wilhelm Peters (1880-1963). Biol. Rundschau 18, 295-300.

• Weiss V. (1981) Der Heritabilitätsindex in der Begabungs- und Eignungsdiagnose bei Kindern und Jugendlichen.Leistungssport 11, 192-195.

• Weiss V. (1982a) Psychogenetik: Humangenetik in Psychologie und Psychiatrie. Fischer, Jena.

• Weiss V. (1982b) Klassischer und probabilistischer Mendelismus: Ein wissenschaftsgeschichtlicher Beitrag zur Latenz wissenschaftlicher Ideen. Biol. Zbl. 101, 597-607.

• Weiss V. (1982c) Major gene locus of Spearman`s general factor of intelligence. Psychol. Rep. 50, 48-50.

• Weiss V. (1984) Psychometric intelligence correlates with interindividual different rates of lipid peroxidation. Biomed. Biochim. Acta 43, 755-763.

• Weiss V. (1985) Mendelian and biometrical approach in sport genetics. In Genetics of Psychomotor Traits in Man (Edited by Wolanski N. and Siniarska A.), pp. 99-104. International Society of Sport Genetics and Somatology, Warsaw.

• Weiss V. (1986) From memory span and mental speed toward the quantum mechanics of intelligence. Person. individ. Diff. 7, 737-749.

• Weiss V. (1987) The quantum mechanics of EEG-brain dynamics and short-term memory. Biol. Zbl. 106, 401-408.

• Weiss V. (1989) From short-term memory capacity toward the EEG resonance code. Person. individ. Diff. 10, 501-508.

• Weiss V. (1990a) The spatial metric of brain underlying the temporal metric of EEG and thought. Gegenbaurs morphol. Jahrb. 136, 79-87.

• Weiss V. (1990b) Social and demographic origins of the European proletariat. Mankind Quart. 31, 127-152.

• Weiss V. (1991) It could be Neo-Lysenkoism, if there was ever a break in continuity! Mankind Quart. 31, 231-253.

• Weiss V. and Mehlhorn H.-G. (1982) Spearmans Generalfaktor der Intelligenz: Genotypen mit ganzzahligen Unterschieden in der zentralen Informationsverarbeitungsgeschwindigkeit. Z. Psychol. 190, 78-93.

• Weiss V., Lehrl S. and Frank H. (1986) Psychogenetik der Intelligenz. Modernes Lernen, 1986.

• Wilson R. S., Rosenbaum G., Brown G., Rourke D., Whitman D. and Grisell J. (1978) An index of premorbid intelligence. J. Consult. Clin. Psychol. 46, 1554-1555.
  
  

  
  

• The bankruptcy of the Plomin approach

  The investigations by Plomin et al. has led to nothing at all. His opinion that high IQ is caused by a very large number of genes each accounting for a very small percentage of variance is nothing else than the declaration of complete bankruptcy of his approach. It is practically equivalent with the politically motivated point of view that there are no genes at all underlying general intelligence. I see no decisive difference.

  Of course, array-based homozygosity mapping of candidate genes regions and high-resolution microarray-based comparative genomic hybridization (array CGH) within consangineous families, in order to detect such regions, needs money and effort. But there seems to be no cheaper way.

  From: Volkmar Weiss [mailto:Volkmar-Weiss@t-online.de]
  Sent: Mittwoch, 21. Januar 2015 10:59
  To: 'James.Sikela@ucdenver.edu'
  Subject: DUF1120 copy number is linearly associated with IQ

  Dear Professor Sikela:

  Yesterday  I read in Human Genetics 134 (2015) 67-75  the full text of your publication on „DUF1220 copy number is linearly associated with increased cognitive function as measured by total IQ and mathematical aptitude scores”,

  see http://www.ncbi.nlm.nih.gov/pubmed/25287832 ,

  full text: https://drive.google.com/file/d/0B3c4TxciNeJZcHg4ek9nWDZGcWs/view?pli=1

  As I did catch sight of your Fig. 2 on page 72 I got deeply impressed, deeply moved, deeply: A linear association between copy arrayCGH based CON2 copy ratio versus WISC IQ, extending in the IQ range between 80 and 140. This is a breakthrough, a centennial breakthrough! My congratulation to your lab and the cooperating colleagues in New Zealand!

  We are aware: What you have discovered is the tip of an iceberg. But it is the tip!

  Your were even clever enough to obtain a patent for the determination of IQ by this copy number variation (CPV),

  see http://www.google.com/patents/WO2014028768A2?cl=en

  DUF means a protein “domain of  unknown function“, containing a number of genes, especially of the NBPF family, each of it highly polymorphic. 

   We need and this research may already under way in your lab:

  1.      Family studies of the inheritance of CON2 copy ratio and IQ. There all  over the world thousands of families with more than one gifted in the IQ range around 130, ready to be  probands.

  2.      Representative population data.

  Until now it was assumed by the majority that IQ differences are caused by thousands of genetic polymorphisms each of it making a small contribution of plus or minus  1, 2  or even3  IQ points. Therefore the environment must play an important or decisive role. Since decades, whoever hinted that this thousand-genes-theory did not agree with the data of segregation of IQ within families, see for example http://www.v-weiss.de/majgenes.html  ,   was seen as an obstinate crank. However, in 1972, already in my  dissertation I wrote that the hypothetical major gene locus of general intelligence could turn out to be a series of alleles. And in 1992: “Of course, the allele M2 could also be understood as an abstraction and be in reality a series of n alleles with small differences; but with a large difference to the M1 allele or an allele-1 series.”  

  The difference between the means of the hypothetical  M1M1 and M2M2 is about 30 IQ points.  This is the range, what you found!  The other hundreds of polygenes which, of course,  influence mental power under certain circumstances may add up to IQ differences of 20 points in extreme and rare cases, but because  the  minor genes are  segregating  independently of each other, their effects as a sum are normally distributed making only a plus or minus of about 5 IQ-points in the general population.

  As we know, in the search for major effects on IQ all  genome-wide association studies (GWAS)  were a failure. Therefore, the conclusion had to be drawn that the explanation had to be found in previously unexplored regions of the genome.

  Therefore, since some years I suggest  to look for copy number variations and the application of homozygosity array mapping within families of the highly gifted. See my monograph “Die Intelligenz und ihre Feinde” (Intelligence and its Enemies). Graz 2012, page 236 to CPV: „Da es sehr gut vorstellbar ist, daß diese Art der genetischen Variabilität auch in der Genetik des normalen IQ eine wichtige Rolle spielt, konzentrieren sich die Hoffnungen gegenwärtig auf weitere Erforschung dieser ‚Copy number variations‘ (CPV).“

  You and your lab had the knowledge. You did it. My congratulation.

  I wish you the possibility, the freedom and the courage to extend your findings. You will need it.

  (I will forward this email to colleagues all over the world. I am sure, they will forward this message further.  What is urgently  needed is deepening of your findings, before the enemies of freedom become aware of the importance of your discovery and are threatening and hampering .)

  Sincerely yours

  Volkmar Weiss

  The mouse has 1 copy of DUF1220, monkeys about 40, chimpanzee 120, homo sapiens nearly 300, with high IQ about 8 more than with low IQ., see

  http://www.collective-evolution.com/2014/10/13/junk-dna-or-does-it-reveal-the-source-of-our-mind-intelligence/

  
  Home