The Advent of a Molecular Genetics of General Intelligence

Published in: Intelligence 20 (1995) 115-124 (Editorial), see also the postscripts (2001; 2003 and 2010 )

Volkmar Weiss

The approach of the IQ Quantitative Trait Loci Project by Plomin et al. (1994) is criticized. Raw scores of IQ test do not exhibit the bell curve, only the normalized scores. Even a bellshaped distribution does not need a large number of underlying genes. Family data are in agreement with Mendelian segregation at a major gene locus of IQ, responsible for the regulation of brain energy metabolism. Therefore, the background of the correlation between glutathione peroxidase activity and IQ should be disentangled, applying methods of molecular genetics.

In 1980 Jensen was of the opinion: "The genotype is itself a theoretical construct. No one can look at a genotype for intelligence under a microscope or isolate it in a test tube" (p. 183). The rapid progress of molecular genetics during the last years has made it possible that the first research report on the molecular genetics of IQ has been published in 1994 by Plomin et al.. This editorial will criticize the approach taken, but with the only aim to make progress in this area of research even more rapid and more straightforward. Since an exhaustive critique of the very popular myth of the bell curve and its underlying genetics has already been published (Weiss, 1992a), we will restrict ourselves here to the most pertinent points.

THE MYTH OF THE BELL CURVE

Plomin et al. (1994) state: "General cognitive ability (intelligence, often indexed by IQ scores) is one of the most highy heritable behavioral dimensions. ... General cognitive ability ... is a quantitative trait with a roughly normal distribution." Of course, normalized by psychologists and definition, respectively. An IQ of 140 compared with an IQ of 70 suggests the double amount or the half of cognitive ability, respectively. However, a look of the raw scores, i.e. of the non-normalized scores, of IQ subtest shows that IQ 140 means an about fourfold amount of cognitive ability compared with IQ 70 (see Table 1). This relationship holds under the condition that all subtests are elementary cognitive tasks and the superior speed of the most intelligent is not clouded by a ceiling effect.

Raw scores of IQ tests do not exhibit the wellknown bellshaped distribution curve, only the normalized scores.

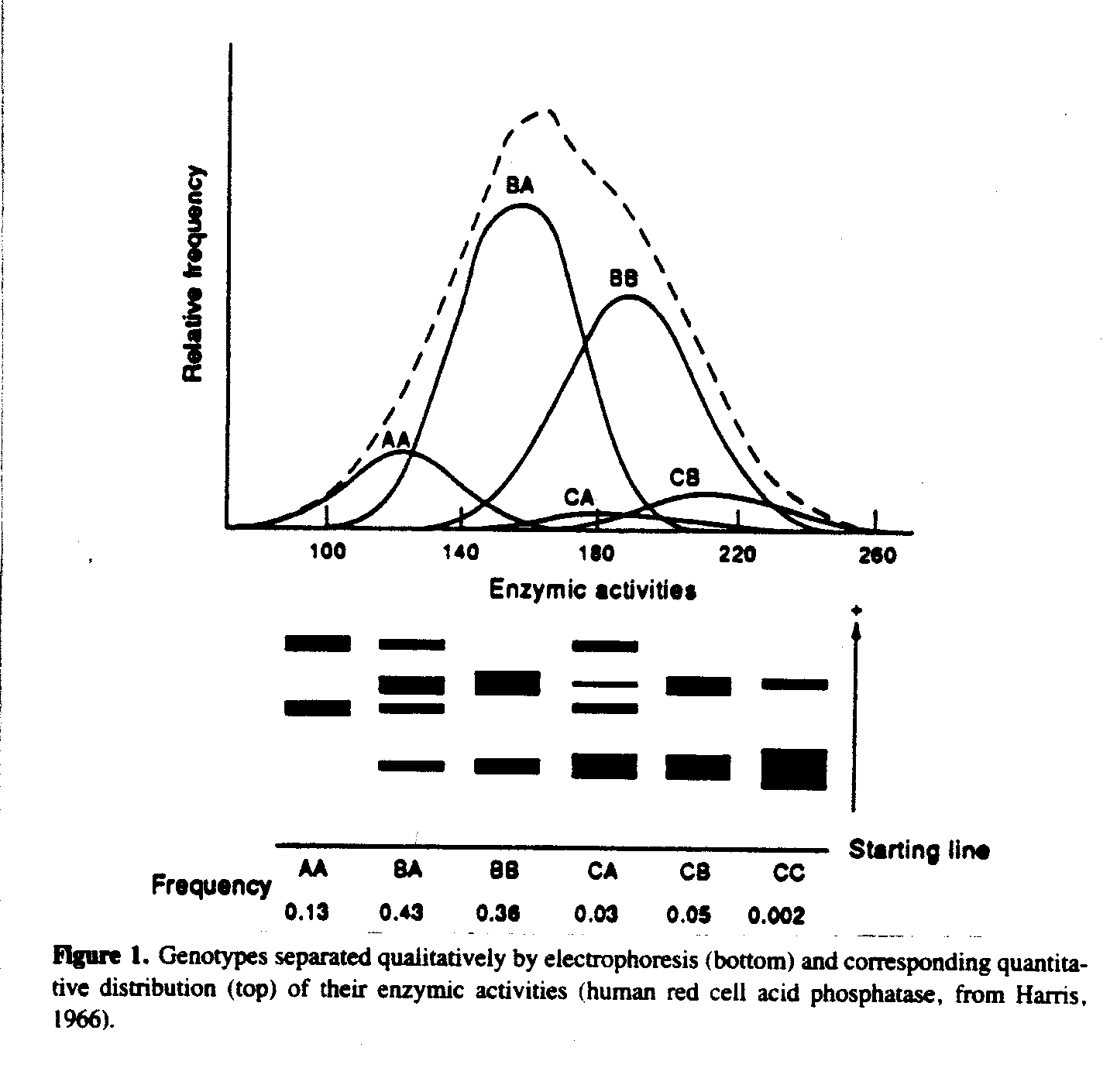
About 1970 geneticists became aware that genotypes, who could be separated qualitatively by electrophoresis of human blood (Harris, 1966), could exhibit quantitatively a normal distribution of enzyme activities. The three alleles A, B and C underlying this distribution (see Fig. 1), fulfill the conditions of Mendelian segregation at one locus. The heritability for this distribution is 0.82 (Eze, Tweedie, Bullen, Wren & Evans, 1974). Now, in 1995, dozens of such cases of normal distributions with a small number of known underlying genotypes could be cited.

A normal distribution does not need a large number of underlying genes. High or low heritability of a variable is no indicator of the number of underlying genes.

A well-confirmed relationship holds between total values and variances of IQ scores: The higher the IQ, the less the variance. The correlation is such a strong one, that the IQ could even be measured only by the scaled variance of repeated tests. Intuitively, we would even predict the reverse relationship: Someone who is solving more elementary cognitive tasks per unit time, should make more errors. But this is not the case. We do not know any simple theory in all of psychology explaining this relationship. However, genetics offers such a theory: In such genetic polymorphisms as in Fig. 1 the mean m2 for the heterozygotes (for example, BA) is intermediate between the means m1 and m3 for the two homozygotes (AA and BB, respectively).

m2 = (m1 + m3)/2

In many genetic polymorphisms the standard deviations are directly proportional to the means (or si/mi, the coefficient of variation, is constant), which are simple manifolds: s1/m1= s2/m2 = s3/m3 = c

This discovery (by Spielman, Harris, Mellmann & Gershowitz, 1978) is one of the tracks leading to an underlying relationship between variance, speed, and frequency of biochemical switching, and on the more reductionist level of physics to a theory of capacity, energy and brain power (Weiss, 1992b).

Low IQ subjects need more units of time to solve a given elementary task, high IQ subjects less time. In such a way the intinuitive expectation, that higher values (more time) should correpond to higher variances, is again confirmed.

Supported by the relationship between EEG parameters and IQ (Weiss, 1992b), is also the conclusion: The molecular background of IQ differences must have something in common with individual differences in the biochemical regulation of brain energy metabolism.

MAJOR GENES VERSUS POLYGENES

If we would try to investigate the genetic background of a construct, called "physical ability for athletics" (for example, for decathlon) the appropriate approach would be clearly a polygenic one. Fundamental speed, long-distance endurance, body height and muscular power are relatively independent major factors of "physical achievement" among a larger number of other factors. However, if we would investigate only the background of the 100 m dash and eliminate influences of body height, the contractibility of muscle fibers underlying fundamental speed could turn out to have a relatively simple genetic background with a major locus. According to Plomin et al. (1994) the genetics of IQ is analogous to the case of "physical ability". But there are a number of reasons (Weiss, 1992a) that the genetics of IQ could be much simpler and a speed (and hence energy) factor with a major locus could play a decisive role. The existence of such a major locus does not mean that the overall number of factors, involving environmental as well as genetic sources of variance, is less than advocated by Plomin et al., but only that the role of one or two factors is greater.

In 1980 (p. 114) Jensen stated: "There are several critical threshholds within the total range of IQ, each having important educational and occupational consequences for the individual. ... The socially and personally most important threshhold regions on the IQ scale are those that differentiate with high probability between persons who because of their level of general mental ability ... can or cannot succeed in the academic or college preparatory curriculum through high school (about 105), and can or cannot graduate from an accredited four-year college with grades that would gratify for admission to a professional or graduate school (about IQ 115)."

In 1970 in former East Germany a family study, starting with 1329 mathematically gifted with an IQ higher than 130, came not only to very similar threshholds but also from a large body of empirical data (for details see Weiss, 1992) to the conclusion that the three overlapping types (M2M2, 68% of the total population, median IQ 94/ M1M2, 27%, median IQ 112 / M1M1, 5%, median IQ 130, mean IQ 139) are segregating in a Mendelian manner. Twenty three years later a follow-up (Weiss, 1994) of the gifted proved Mendelian segregation among their children (see Table 2) and among their nephews and nieces. Of course, in social reality, where cognitive ability is embedded into personality and chance plays its role in each biography, a 100% fit between a Mendelian theory of IQ and empirical results cannot be expected.

Where polygenic theory predicts a normal distribution of ability among siblings of the same family (Jensen 1980, p. 80), major gene theory predicts that the IQ distribution of the offspring of homozygotes and their M1M2-spouses should be quite markedly skewed (compare Table 2, second row). The skewness should be in the opposite direction for M1M1-M1M2 offspring compared to M2M2-M1M2 offspring (compare Table 3, second and fourth row). M1M2-M1M2 offspring, who is segregating according to the Mendelian rules, should have a much greater variance than the offspring of marriages, where both partners are homozygotes and are "breeding true" (compare Table 3, first, third and fifth row), that means only with regression to the mean of the specific type. The major gene effects should even be more pronounced if we compare not-normalized raw scores instead of IQ values.

From the strong relationship between mean and variances of raw scores, an exact prediction of the variance for each of the cells of Table 2 and 3 is possible. Another prediction of major gene theory of intelligence that the means of raw scores of genotypes are simple manifolds, had already been confirmed by Frank (1985). Since 1959 Frank (see Lehrl, Gallwitz, Blaha & Fischer, 1991, for the last updating of Frank`s theory and for representative empirical results) is claiming that general cognitive ability is limited by the channel capacity of short-term memory (Kyllonen & Christal, 1990). Frank and and his school (Lehrl & Fischer, 1990; Weiss, 1992b) are arguing that the capacity C of short-term memory (measured in bits of information) is the product of the processing speed S of information flow (in bits/s) and the duration time D (in s) of information in short-term memory.

Hence

C (bits) = S (bits/s) x D (s)

According to Frank (1985) the mean of M1M1 is 140 bits, and of M2M2 70 bits, that means the contribution of a single M1 allele to short-term memory storage capacity C is about 70 bits, of a M2 allele about 35 bits. For a heterozygote M1M2 hence 70 bits + 35 bits = 105 bits. By Lehrl et al. testing of processing speed S was operationalized by reading rates, duration of information D by memory span. - see: The Basic Period of Individual Mental Speed (BIP)

In 1993 in the follow-up sample (Weiss, 1994) 97% (n = 357) of the highly gifted M1M1- males were in professions typically associated with an IQ above 123, compared with 55% (n =77) of the sons, 49% (n =220) of the brothers, 40% (n =346) of the fathers, 18% (n =570) of the male cousins, 22% (n =76) of the nephews, 14% (n=615) of the uncles (these data from 1971), 11% (n =2250) of the male cousins of the parents (with no evidence for any excess on the paternal or maternal side and hence no evidence for X-chromosome linked inheritance), 9% (n = 681) of the grandfathers, 5% (n =1996) of the uncles of parents and 4% (n =1290) of the greatgrandfathers. None of the major psychoses has such a high and regular "recurrence risk" among relatives as giftedness.

Drawing our results (Weiss, 1992a, 1994) into consideration, the research design by Plomin et al. (1994) was not optimal. The samples representing the top 5% (average IQ of 130) and top 1% (average IQ of 142) are quite right, as it is the idea of the comparison of extreme groups. However, the group of children with scores near the mean (average IQ of 105) is a mixture of M1M2 and M2M2 individuals, an average IQ of about 112 would have been more appropriate. Results from the bottom 5% and even 1% of the normal IQ distribution can be misleading, far better would be a representative sample from about the 40% lower tail of the IQ distribution (avoiding in such a way overlapping with M1M2 individuals). From the point of major gene theory the bottom 5% should even be avoided, because in this range of scores the effects of a large number of rare alleles can expected, which drastically disturb cognitive development, but do not play an important role beyond this range of scores.

WHY NOT GLUTATHIONE PEROXIDASE?

Since in November 1970 I had calculated the first table, suggesting Mendelian segregation of IQ at a major locus (see Weiss, 1992a), it was my declaired aim to promote the discovery of the underlying polymorphism. All over the world IQ and intellectual achievement are more or less correlated with income and social status. Therefore, the wanted polymorphism should also be correlated with social status. However, the poor and the rich are not only differentiated by their average IQ, but also more or less dramatically by their living conditions and hence their conditions for Darwinian selection. The polygenic approach should run into this trap and produce a number of "polygenes of IQ" (the new HLA marker for a gene unique to the human brain could be the first one; see Plomin et. al. 1994), not connected with cognition at all, but reflecting different selection pressures (for example, for immunological factors) among the social strata. Association does not necessarily imply causation. Assortment of some genes (causing myopia, for example) could last over generations and accumulate different alleles in different social strata.

The first report of the IQ Quantiative Trait Loci (QTL) Project (Plomin et al., 1994) presents allelic association results for 60 markers. For two-allele markers allelic frequency differences between the low- and high-IQ groups of about .20 are significant. The only difference near significance, which from my point of view is exciting, is the small association found between IQ and mitochondrial superoxide dismutase 2. - From the point of major gene theory for the wanted locus an allelic frequency of 1.OO for the top IQ group would be predicted and of about .02 for the bottom group. For a discovery with such clearcut contours we should strive for.

In 1982 I became aware (see Weiss, 1984) of a paper published by Sinet, Lejeune & Jerome (1979) in which a correlation of .58 between IQ and erythrocyte glutathione peroxidase activity (GSHPx) was reported for 50 trisomy 21 patients. None of the other enzymes studied correlated with IQ. Sinet et al. thought the correlation to be trisomy-specific, because an increase of about 50% in the superoxide dismutase activity (SOD-1) can be observed in cells from trisomy 21 patients. There is a feedback control of GSHPx concentration by the amount of superoxide, which explains (Chan, Yu, Chen & Epstein 1989) the elevated activity of GSHPx in cells of trisomy 21 patients. However, Fraser and Sadovnick (1976) had found that the correlations of IQ between trisomy 21 probands with their fathers, mothers and sibs are about .50, consequently of the same size as with healthy children despite the mean IQ of trisomy 21 probands being about 70 points lower. Therefore already Lenz (1978) had concluded that individual differences in trisomy-IQ have generally the same biochemical background as in normal persons. And Brugge, Nichols, Delis, Saitoh & Truaner (1992) confirmed a correlation of .73 between erythrocyte GSHPx activity and a short-term memory score.

Because of the political situtation in former East Germany, since 1982 the author of this editorial had lost all possibilities (see Weiss, 1991) to promote investigation into these correlations with a laboratory background of his own, and he could accumulate only indirect evidence (Weiss, 1984, 1992a).

We all know that an occupational group with higher education, whether black, white or yellow, has a mean IQ of at least 30 points higher than the social stratum of unskilled workers. Up to World War One for historical reasons Germans in the Baltic States were nearly all members of the former ruling upper stratum; and now the about 50 000 Baltic Germans, resettled in Germany, are a cultural community far above average. In 1913, a representative comparison of IQ sampled in Estonia, would have had the false result that Germans are about one standard deviation of IQ higher than Estonians. Therefore, I conclude that nations or races could only be compared if all social positions are filled by one race (as in Nigeria and Sweden). In all other cases, IQ-differences are mixed up with the consequences of social inequality or are themselves the cause of inequality. With this in mind, we look at the following data: Golan, Ben Ezzer & Szeinberg (1980) published findings on a quantitative genetic polymorphism of erythrocyte GSHPx actitivity. The population mean of Jews in Israel was 23,7 + 7,0 U GSHpx/Hb. By Gerli, Mongiat, Gualandri, Orsini & Porta (1984) GSHPx was assayed in families of Mediterranean origin (population mean of about 20 + 5 U) and the results support the existence of two Mendelian alleles. Mean GSHPx activity among Australian aborigines is 12,6 +3 U (Agar, Gupta, Gruca & Welch, 1980). 100 healthy university student had a mean of 40,5 + 11,9 U (Lane, Dudrick & Warren, 1981). However, there are differences between the methods used, and the results can only be only tentative.

Also glutathione S-transferases (GST) possess GSH peroxidase properties (see, for example, Saneto, Awasthi & Srivastava, 1982). GST is a whole family of genetic polymorphisms, and at least one new polymorphism is discovered each year. However, until now we do not know anything about the contribution of any GST-polymorphism to the correlation between GSHPx and IQ. The molecular genetics of GSHPx and GST polymorphisms is in rapid development, and many locations on chromosomes are well known. A research group, who wants to contribute to this area, will have to refer to the most actual electronic data base.

At the beginning (Weiss, 1984) GSHPx seemed only to be involved with lipid peroxidation. However, the disvovery of the regulation of the NMDA receptor-channel complex (Sucher & Lipton, 1991) by oxidized glutathione has opened a new research front. The involvement of the NMDA complex in short-term memory and long-term potentiation is one of the hottest fields of neurochemical research. In view of this direct and indirect evidence, it is to complain that Plomin et al. did not investigate GSHPx or the family of GST polymorphisms until now.

Among the polygenes of IQ, one will turn out to have the largest effect. By definition it will be the major gene locus. Whether approach will be taken, either a search for polygenes or an approach, led by major gene theory, the result of replicable science must finally be the same. One of the minor genes of IQ (at least for the eldery), already discovered, is apolipoprotein E (Goedert, Strittmater & Roses, 1994). Considering the public opinion on this subject (Weiss, 1991) in general, nobody, however, would have got the money for a major gene approach as early as 1990. From this point of view the IQ QTL project (Plomin et al., 1994) has always to be understood as a breaktrough.

REFERENCES

• Agar, N. S., Gupta, J. D., Gruca, M. A. & Welch, J. S. (1980). Levels of glycolytic enzymes in the red blood cells of Australian aborigines Enzyme, 25, 329-332.

• Brugge, K. L., Nichols, S., Delis, D., Saitoh, T. & D. Truaner (1992). The role of alterations in free radical metabolism in mediating cognitive impairment in Down`s syndrome. In J. Emerit and B. Chance (Eds.), Free radicals and aging. Basel: Birkhäuser.

• Chan, P. H., Yu, A. C. H., Chen, S. & Epstein, C. J. (1989). Oxidative stress exacebrates cellular damage in primary cultures of astrocytes from human SOD1 transgenic mice. Journal of Cell Biology, 107, 726a.

• Eze, L. C., Tweedie, M. C. K., Bullen, M. F., Wren, P. J. J. & Evans, D. A. P. (1974). Quantitative genetics of human red cell phosphatase. Annals of Human Genetics, 37, 333-340.

• Frank, H. (1985). Is intelligence mesurable and is it inherited? Folia Humanistica, 23, 671-691.

• Fraser, F. C. & Sadovnick, A. D. (1976). Correlation of IQ in subjects with Down syndrome and their parents and sibs. Journal of Mental Deficiency Research, 29, 179-182.

• Gerli, G. C., Mongiat, R., Gualandri, V., Orsini, G. B. & Porta, E. (1984). Erythrocyte glutathione peroxidase in subjects of mediterranean origin. Human Heredity, 34, 133-140.

• Goedert, M., Strittmater, W. J. & Roses A. D. (1994). Risky apolipoprotein in the brain. Nature, 372, 45-46.

• Golan, R., Ben Ezzer, J. & Szeinberg, A. (1980) Red cell glutathione peroxidase in various Jewish ethnic groups in Israel. Human Heredity, 30, 136-141.

• Harris, H. (1966). Enzyme polymorphisms in man. Proceedings of the Royal Society of London, B164, 298-310.

• Horn, W. (1962). Leistungsprüfsystem (LPS). Göttingen: Hogrefe.

• Jensen, A. R. (1980). Bias in mental testing. London: Methuen.

• Kyllonen, P. C, & Christal, R. E. (1990). Reasoning ability is (little more than) working memory capacity. Intelligence, 14, 389-433.

• Lane, H. W., Dudrick, S. & Warren, D. C. (1981). Blood selenium level and glutathione-peroxidase activities in university and chronic intravenous hyperalimentation subjects. Proceedings of the Society for Experimental Biology and Medicine, 167, 383-390.

• Lehrl, S. & Fischer, B. (1990). A basic information psychological parameter (BIP) for the reconstruction of concepts of intelligence. European Journal of Personality, 4, 259-286. - see: The Basic Period of Individual Mental Speed (BIP)

• Lehrl, S., Gallwitz, A., Blaha, L. & Fischer, B. (1991). Geistige Leistungsfähigkeit. Theorie und Messung der biologischen Intelligenz mit dem Kurztest KAI. Ebersberg: Vless.

• Lenz, W. (1978). Humangenetik in Psychologie und Psychiatrie. Heidelberg: Quelle und Meyer.

• Plomin, R., McClearn G. E., Smith, D. L., Vignetti, S., Chorney, M. J., Chorney, K., Venditti, C. P., Kasarda, S., Thompson, L. A., Detterman, D. K., Daniels, J., Owen, M. & McGuffin, P. (1994). DNA markers associated with high versus low IQ: The IQ quantitative trait loci (QTL) project. Behavior Genetics, 24, 107-118.

• Saneto, R. P., Awasthi, Y. C. & S. K. Srivastava (1982). Glutathione S-transferase of the bovine retina. Evidence that glutathione peroxidase activity is the result of glutathione S-transferase. Biochemical Journal, 205, 213-217.

• Sinet, P.-M., Lejeune, J. & Jerome, H. (1979). Trisomy 21 (Down`s syndrome), glutathione peroxidase, hexose monophosphate shunt and I.Q.. Life Sciences, 24, 29-34.

• Spielman, R. S., Harris, H., Mellmann, W. J. & Gershowitz, H. (1978). Dissection of a continuous distribution: Red cell galactokinase activity in blacks. American Journal of Human Genetics, 30, 237-248.

• Sucher, N. J. & Lipton, S. A. (1991). Redox modulatory site of the NMDA receptor-channel complex: Regulation by oxidized glutathione. Journal of Neuroscience Research, 30, 582-590.

• Weiss, V. (1984). Psychometric intelligence correlates with interindividual different rates of lipid peroxidation. Biomedica Biochimica Acta, 43, 755-763.

• Weiss, V. (1991) It could be Neo-Lysenkoism, if there was ever a break in continuity! Mankind Quarterly, 31, 231-253.

• Weiss, V. (1992a). Major genes of general intelligence. Personality and individual Differences, 13, 1115-1134.

• Weiss, V. (1992b). The relationship between short-term memory capacity and EEG power spectral density. Biological Cybernetics, 68, 165-172.

• Weiss, V. (1994). Mathematical giftedness and family relationship. European Journal for High Ability, 5, 58-67.
  
  P.S. (2001) After publication of this paper, in 1996 (and newly discovered polymorphisms again in 2000, but not GSTO1) all known polymorphisms of GST and GSHPx, now GPX, were tested for any relationship with IQ by five independent research groups and nothing was found at all. (These negative findings were not published.) Until now, we do not know any reasonable explanation for the reported correlations, too. We have to assume that a genetic polymorphism in a still unknown regulation of methionine and nitrosoglutathione metabolism could be the underlying cause. – In the meantime, Plomin et al. were also busy. In 2001 they published the results of “A genome wide scan of 1842 DNA markers for allelic associations with general cognitive ability”. They, too, found nothing at all. Their socalled QTLs account for less than a 1% of the variance. Such a ridiculous amount cannot explain the facts of IQ-segregation and social mobility in human societies, hinting strongly to the existence of a major gene locus. See also www.v-weiss.de/table.html . It will be a matter of time and diligence, then we all will be wiser. V.W.
  
  P.S. (2003) The discovery of targets for memory enhancing drugs by discovering the genetic background of IQ 

  In February 2003 the discovery of the genes underlying taste sensitivity to phenylthiocarbamide (PTC) was published by D. Drayna and coworkers. In 1969 during my first empirical study I tested several hundred subjects for their ability to taste PTC, and I tried to find the optimal threshold to separate the overlapping distributions of tasters from non-tasters. Since 1931 many authors believed that a simple two-allele model of a single locus could fit the genetics of PTC-tasting sensitivity. However, I remember vividly a case in the village, where my wife comes from and where I tested the whole population, that in one family either the genetic model was wrong or one child illegitimate. The most simple explanation for such irregularities has always been the hypothetical existence of a third allele with low frequency. Indeed, such an allele has now been discovered by molecular genetics. However, because the distribution of PTC-tasting sensitivity is a quantitative one, in the meantime some authors had rejected the simple major gene model. Heritabilities were calculated, models of polygenic inheritance were advocated and occam’s razor was replaced by the usual nonsense of argumentation and counterargumention. Therefore, for me, the discovery by Drayna is not only a triumph of science, but also a model of hope.  

  Already in November 1990 I came on the basis of empirical data to the conclusion that a major gene of IQ must exist (see www.v-weiss.de/majgenes.html  and www.v-weiss.de/ability.html ). Where there is segregation within families following Mendelian rules there must be a underlying gene locus causing this segregation, and such a locus can be discovered (see www.v-weiss.de/intellig.html ).  This is the iron logic of genetics.  But in contrast to PTC the genetics of IQ is a political problem, too (see www.v-weiss.de/lysenkoism.html ). For example, Plomin was invited to Leipzig by psychologists and I was eyewitness of his presentation. The counterlogic of Neo-Marxists against the genetics of IQ is a simple one: Because the mere existence of genes can no longer be denied, in the case of IQ the importance of such genes should be minimized. The importance of genes becomes a minimum, if there is a very large and undetermined number of genes underlying the character, if there is a large influence of nurture and environment and if there is such an error of measurement that IQ scores are meaningless. And last but not least, the concept of general intelligence is at no value at all, because there are a plethora of “intelligences”. The last does Plomin not say, but he is serving the first two prejudices of egalitarian ideology very well, and he is, therefore, applauded by the audiences of the present Zeitgeist. With their needle-in-the-haystack-searching-method Plomin et al. have found nearly nothing during 15 years of research.

  Reason enough, to see in him the most visible representative of any genetics of IQ, then there should be nothing. But when the effort and the methodological sophistication applied in the case of PTC-tasting sensitivity would be applied to the genetics of general cognitive ability, too, we will obtain a similar result within a comparable time span. Time is ripe now for such an approach. If you have only two men, a very intelligent one with an IQ of 135 and a mentally healthy one with an IQ of about 90, and you decode the sequences of these two men, there where the intelligent one is different from the less intelligent on both chromosomes, there could be the locus of IQ. To exclude decoding errors you need not one but about 5 men of each mental class.

  On the genetic level the difference between an intelligent man and a less intelligent is not a matter of quantity, but of quality. For practical and ideological reason the aim of research should not be the genetical background of IQ, but the genetics of short term memory capacity, earlier or later onset of Alzheimer and the discovery of targets for memory enhancing drugs. V.W.

  Percentage of higly gifted and high IQ subjects among the relatives of highly gifted

  
  Charles Spearman: "General intelligence," objectively determined and measured.
  

  
  

  Progress in the genetics of autosomal recessive nonsyndromic mental retardation (ARNSMR)

  Volkmar Weiss

  Home

  In 2009 the combination of autozygosity mapping and microarray RNA expression analysis has led to the discovery of new genetic polymorphisms underlying nonsyndromal intellectual disability (ARNSID) with autosomal recessive inheritance. We can be convinced that the application of similar methods to consanguineous families with several members in the high IQ range will lead to the discovery of copy number variations and other gene polymorphisms underlying the variability of IQ in the upper and normal range of the IQ distribution. Time and methods are ripe for such an approach.

  ARNSMR polymorphisms can be understood as a bridge to IQ variation in the normal range. However, for example, until now nothing is known on the correlation of IQ with common polymorphisms of the human cereblon gene (CRBN). Higgins et al. did nothing publish about the mean IQ of heterozygotes of the mutation in the CRBN gene, whose homozygotes have an IQ between 50 and 70.

  To date (February 2010), about 20 ARNSMR loci have been mapped and four genes identified. The ARSNMR causing genes belong to different protein families, including serine proteases, adenosine 5'-triphosphate-dependent Lon proteases and calcium-regulated transcriptional repressors. All of the mutations in the ARNSMR-causing genes are protein truncating, indicating a severe loss-of-function effect. Analogous polymorphisms can be assumed to be underlying IQ in the normal range of distribution between IQ 70 and 140.

  NRG1, Neuregulin 1, rs392499

  The paper by J. Hall et al., published online 29 October 2006 in Nature Neuroscience http://www.nature.com/neuro/journal/vaop/ncurrent/abs/nn1795.html, shows that a variant of NRG1, a susceptibility gene for schizophrenia, is associated with premorbid IQ.
  

  Since years I am routinely checking any association or correlation between a gene and IQ whether the allele frequencies of a nonsynonymously coding polymorphism could fit the allele frequencies of a major gene of general intelligence or not. From a large body of empirical data I have drawn the conclusion, see www.v-weiss.de/majgenes.html , that the allele frequency of the allele underlying a high IQ should be about 0.20 in representative Eurasian samples with a mean IQ of 100, about 0.01 among African blacks, and about 0.06  among US-American blacks. If the data of a century of IQ testing are not complete nonsense – see www.v-weiss.de/calibration.html - there should be a striking difference in allele frequencies between Eurasians on the one hand and Blacks of the other.
  

  NRG1 has only one common polymorphism, coding nonsynonymously, namely rs3924999 with alleles C/T, see  http://www.ncbi.nlm.nih.gov/SNP/snp_ref.cgi?rs=3924999 .  This SNP exhibits striking racial differences. In the HapMap samples the frequency of the T allele among Europeans is 0.36, among Asian about 0.79, among Sub-Saharan Blacks 0.02, among African American  0.11. However, you should be aware that the Asian samples were drawn from the inhabitants aof Tokyo, Beijing and Los Angeles. The Chinese HapMap-HCB sample comprises even a Beijing university resident academic population where the hypothetical homozygous low IQ-typ CC of the ancestral allele could  be expected only among subjects of the technical staff. With other words: The Asian samples are not socially representative in any way, and I have my doubts that the European sample is socially representative.  Under the assumption of a correlation between this SNP and IQ and hence social status, the T allele should be overrepresented in the Asian samples to a high degree. In most cases heterozygotes of this allele should have an IQ above 105, homozygotes above 124.
  

  Until now, association studies with NRG1 are burdened with a lot of controversial results. The problems of replication  may not only be caused by large population and racial differences, see the article by Gardner, M. et al.: Extreme populations difference across Neuregulin 1 gene. Molecular Psychiatry 11 (2006) 66-75, see http://www.nature.com/mp/journal/v11/n1/abs/4001749a.html  but also by social stratification of allele frequencies.

  However, another and even more important problem seems to be the copy number variation of this gene, especially around rs392499, causing methodological challenges of a new and unexpected magnitude. What is needed to overcome these challenges is array-based homozygosity mapping and high-resolution microarray-based comparative genomic hybridization (array CGH) within consangineous families, see http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&dopt=Abstract&list_uids=16311745&query_hl=11  comprising a number of probands with an IQ above 124.

  The investigation of pooled DNA samples by Plomin et al. has led to nothing at all, not even his 500K study. His opinion that high IQ is caused by a very large number of genes each accounting for a very small percentage of variance is nothing else than the declaration of complete bankruptcy of his approach. It is practically equivalent with the politically motivated point of view that there are no genes at all underlying general intelligence. I see no decisive difference.

  Of course, array-based homozygosity mapping of candidate genes regions and high-resolution microarray-based comparative genomic hybridization (array CGH) within consangineous families, in order to detect such regions, needs fare more money and effort than investigating pooled DNA.

   

  miRNA, Trinucleotide Repeats, Glutathione Status and the Genetics of IQ

  Volkmar Weiss

   Home

  Until now, more than 1 000 000 SNPs have already been investigated for an association with IQ by Plomin, Deary et al. and others. No major effect has been discovered which could explain the high heritabiltiy of general cognitive ability and the pattern of Mendelian segregation of IQ in the normal range of variation. Plomin et al. found only very small and mostly non-replicable effects. Therefore, our mind should be open for a broader outlook and new hypotheses.

  MicroRNAs as regulatory factors in gene expression renders them attractive candidates for harbouring genetic variants with effects on IQ. There is already ample evidence that miRNA-mediated gene regulation plays an important role in a number of neurodegenerative diseases. MiRNAs bind to complementary sequences in the three prime untranslated regions (3' UTRs) of target messenger RNA transcripts. MiRNA genes are found in intergenic regions or in anti-sense orientation to genes and contain their own miRNA gene promoter and regulatory units. As much as 40% of miRNA genes may lie in the near-gene introns of protein and non-protein coding genes or even in exons.

  Our first example:

  Harold, D. et al., Nature Genetics 41 (2009) 1088ff. have found out and replicated compelling evidence that rs3851179 of the PICALM gene is associated with alzheimer. The homozygotes and heterozygotes of the rare allele A of rs3851179 have a 0,86x decreased risk for alzheimer. - Since many years I am looking for such findings, because we should expect that probands of high general intelligence (high IQ) have a later onset of alzheimer and a decreased risk. Surprisingly, the allele frequencies not only of rs3851179, but even more of rs669556 and of at least 30 other SNPs in this near gene region exhibit the frequencies of a hypothetical major gene locus of general intelligence, see http://www.v-weiss.de/majgenes.html and http://knol.google.com/k/national-iq-means#
  
  As it seems, at the moment, nobody has an explanation why the non-coding SNP rs3851179 is associated with alzheimer and why in a large chunk of DNA with copy number variation a high number of SNPs exhibits similar allele frequencies in all the populations of the HapMap project. In which way could such a phenomenon have been stabilized by natural selection? Could this region be coding for miRNA or be its binding target?
  

  The second example:

  By checking routinely the bibliographical details of paper published together with A. Payton et al. on "Investigation of a functional quinine oxireductase (NQO2) polymorphism and cognitive decline" in  Neurobiol. Aging 31 (2010) 351,  I became aware of a publication on "Genetic variant
  of glutathione peroxidase 1 in autism" Brain Dev. 32 (2010) 105
  

  Since 1982 I did collect evidence on a relationship between glutathione peroxidase activity, general cognitive ability (IQ) and social status (for example, measured by years of education as a good surrogate).  I quote in the following from an editorial published by me 1994 in the journal "Intelligence":
  

  "In 1982 I became aware of a paper published by Sinet, Lejeune & Jerome (1979) in which a correlation of .58 between IQ and erythrocyte glutathione peroxidase activity (GSHPx, now GPX1) was reported for 50 trisomy 21 patients. None of the other enzymes studied correlated with IQ. Sinet et al. thought the correlation to be trisomy-specific, because an increase of about 50% in the superoxide dismutase activity (SOD-1) can be observed in cells from trisomy 21 patients. There is a feedback control of GSHPx concentration by the amount of superoxide, which explains the elevated activity of GSHPx in cells of trisomy 21 patients. However, Fraser and Sadovnick (1976) had found that the correlations of IQ between trisomy 21 probands with their fathers, mothers and sibs are about .50, consequently of the same size as with healthy  children despite the mean IQ of trisomy 21 probands being about 70 points lower. Therefore already Lenz (1978) had concluded that individual differences in trisomy-IQ have generally the same biochemical background as in normal persons. And Brugge et al. (1992) confirmed a correlation of .73 between erythrocyte GSHPxactivity anda short-term memory score. ...  By Gerli et al. (1984) GSHPx was assayed in families and the results support the existence of two Mendelian alleles.?  For the full text see http://www.v-weiss.de/intellig.html
  

  In the following years I instigated a number of colleagues from all over the  world to discover the underlying genetic cause of the cited correlations, but nearly completely in vain. We investigated SNPs of GST transferases, NQO and many, many others. Therefore I came to the conclusion that the major contribution to the correlation between lipid peroxidation and IQ could or should be the effect of a gene with copy number variations and repeat polymorphisms for which data are still not available or incomplete.
  

  In April 2010, at the present state of knowledge, GPX1 is such a gene for which at least 4 common frameshift polymorphisms are already known. The arguments in favor of a relationship between trinucleotide repeat polymorphisms of GPX1 and general cognitive ability are holding for GCLC and its GAG-repeat polymorphism, too. GCLC influences the glutathione status of an individual to a high degree. The GCLC repeat polymorphism with its known large population differences in allele frequences is located in the three prime untranslated region (3' UTR) and therefore a likely binding target of a miRNA! In view of the claimed relationship of GSH/GSSG redox status with schizophrenia and other neurodegenerative diseases, we should be eager to see whether a correlation between GCLC GAG-repeat status and general cognitive ability can be confirmed or not, see
  http://www.google.de/search?hl=de&source=hp&q=GCLC+GAG-repeat&btnG=Google-Suche&meta=&aq=f&aqi=&aql=&oq=&gs_rfai

  As I see, new publications and reviews on the relationship between glutathione status and brain function are not aware of some older publications. In the appendix ?Memory as a Macroscopic Ordered State by Entrainment and Resonance in Energy Pathways?, pp. 201-221, of the monograph "Psychogenetik der Intelligenz?. Dortmund. Verlag Modernes Lernen 1986, I wrote on p. 210ff:

  "It would defy the most fundamental laws of thermodynamics, when individual differences in brain power would not find their counterpart in individual differences of brain energy metabolism. ? Reactions involving S-S or S-H groups of proteins may readily account for the apparently opposite effects of the same control mechanism.  ? . At this point we direct attention to the correlation (.58) between IQ and glutathione peroxidase (GSHPx, now GPX) activity (SINET et. 1979) ? In modulating the GSH/GSSG ratio, GSHPx not only contributes to the regulation of glycolysis (GILBERT 1984) but consequently also the adenylate energy charge (REHNCRONA et al. 1980) and the NADP/NADPH ratio (GRIMM 1978) are prefectly correlated (r = 1.00!) with glutathione status. Thus the fundamental chemical needs of a living cell, high-energy phosphate stores (ATP) and reducing power (NADPH) depend upon the cortical concentration of glutathione, and the dynamic behavior of a complex system can be reduced to the molecular properties of a master enzyme in an energy pathway."

  The combination of autozygosity mapping and microarray RNA expression analysis has led to the discovery of new genetic polymorphisms underlying nonsyndromic mental retardation with autosomal-recessive inheritance, see http://www.medicalnewstoday.com/articles/174204.php  and
  http://www.cell.com/AJHG/abstract/S0002-9297(09)00522-9
  We can be convinced that the application of similar methods to consanguineous families with several members in the high IQ range will lead to the discovery of gene polymorphisms underlying variability of IQ in the upper and normal range of the distribution.  Sites where miRNA is coded or binding and these are especially regions with trinucleotid repeats in the 3?UTRs as GCLC should be investigated as soon as possible.

  For all such neurodegenerative diseases as schizophrenia, autism, alzheimer and so on general cognitive ability (IQ) has to be seen as a major confounding variable, and nobody will obtain clearcut results in the genetics of neurodegenerative diseases as long as the genetic background of IQ in the normal range of variation remains unknown.

  I thank my eldest daughter, Dr. Cornelia Weiss-Haljiti, for helpful discussions, Easter 2010.

  Home