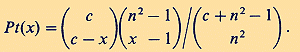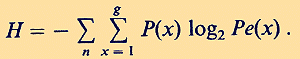
Home
other publications

German Central Office for Genealogy

Die IQ-Falle



E-Mail




Last update 12/2004

VOLKMAR WEISS
Der IQ-Fallensteller

The IQ-Trapper
IQ, Short Term Memory, Attention, and the Code of the Brain

Where you are reading Pi (3,14) in the following paper from 1992, you should replace Pi by 2 Phi (3,236) -

see: Weiss, Harald and Volkmar Weiss: The golden mean as clock cycle of brain waves. Chaos, Solitons and Fractals 18 (2003) 643-652 - Elsevier Author Gateway, online version -

or v-weiss/chaos.html

-------------------------------------------------------------------------------------------------

published in: Biological Cybernetics 68 (1992)165-172

The Relationship between Short-Term Memory Capacity

and EEG Power Spectral Density

Volkmar Weiss

Abstract. Multiplying memory span by mental speed, we obtain the information entropy of short-term memory capacity, which is rate-limiting for cognitive functions and corresponds with EEG power spectral density. The number of EEG harmonics (n = 1, 2, ... , 9) is identical with memory span, and the eigenvalues of the EEG impulse response are represented by the zero-crossings up to the convolved fundamental, the P300. In analogy to quantum mechanics the brain seems to be an ideal detector simply measuring the energy of wave formes. No matter what the stimulus is and how the brain behaves, the metric of signal and memory can always be understood as a superposition of np states of different energy and their eigenvalues.


1 Introduction
During the last decade a number of papers and books have been published, claiming in a more or less speculative manner (for the current state of this art compare Penrose 1990) a link between quantum mechanics and thought. Koenderink and Van Doorn (1990) even found a "miraculous coincidence" between their partial differential equations of receptive fields of vision and the harmonic oscillator of quantum mechanics. And Vichnevetsky discovered (1988) by simulation experiments "unexpectedly that wave propagation in computational fluid dynamics and the motion of particles in quantum mechanics share similar mathematics". However, all these authors are seemingly unaware of a growing body of empirical evidence, interpreted in the following and supporting their arguments.

Already in 1966, Kac, had put forward the question: Can one hear the shape of a drum? In order to find an answer, Kac asks for the energy in the frequency interval df. To this end, he calculates the number of harmonics which lie between the frequencies f und df and multiplies this number by the energy which belongs to the frequency f, and which according to the theory of quantum mechanics is the same for all frequencies. By solving the eigenvalue problem of the wave equation, Kac is able to state that one can not only hear the area of a reflecting surface, its volume and circumference, but also - and this seems to be the most exciting result in view of modern network theories of brain machinery - the connectivity of paths of an irregular shaped network. If the brain waves had the possibility to measure and hence to "know" the eigenvalues of a spatially distributed information amount, they would have nearly perfect access to information and - in terms of communication theory - perform nearly perfect bandlimited processing. As we know, the eigenvalues are proportional to the squares (i.e. variances) of resonant frequencies (Fogleman 1987).

The question whether brain waves reflect underlying information processing is as old as EEG research itself. Such relationships between well-confirmed psychometric and psychophysiological empirical facts (compare also Eysenck 1986 and 1987) and EEG spectral density, and why, are the very problem. Recently, Resnikoff (1989) has published a textbook which contains the background of interdisciplinary knowledge, indispensible for progress in a field of such sophistication.


2 Empirical Results of NeoPiagetian Cognitive Psychology

Ever since short-term memory became the object of scientific study, psychologists have recognised that it possesses a quantitative dimension in terms of the maximum number of items to which a person can attend at one time. Attempts to measure this span of attention revealed that it was indeed limited, but that those limits were fluid and depended on a variety of factors. However, the discovery of a constant in science, even a "fuzzy" one, is an important event. It now seems almost universally accepted that short-term memory span has a capacity limit of seven plus or minus two (Miller 1956). The possibility that such quantitative limits on attention span might be related to qualitative differences in thought and reasoning was recognised by Piaget (see 1971) in his earliest research reports. Beginning with Pascual-Leone (1970), the prediction of children`s reasoning from estimates of their memory span has been a major goal of neoPiagetian theories of cognitive development.

In the pioneering research by Pascual-Leone (1970) the maximum of memory span became the mental energy operator M. Maximum mental power (= M) is characterised as the maximum absolute number of different schemes (including overlearned complex subroutines and strategies) that can be activated in a single mental act. Pascual-Leone (1970; p. 304) understands memory span as the maximum of discrete and equal energy units (i.e. quanta) which every subject has at his disposal. "Assuming that M operates upon the units or behavioural segments available in the subject`s repertoire, as the repertoire changes with learning so will the level of performance even if the subject`s M value remains constant. A distinction can and should be made between the subject`s maximum capacity or structural M (Ms) and his functional M (Mf) or amount of Ms space actually used by him at any particular moment of his cognitive activity. It seems reasonable to assume that the value taken by Mf oscillates between zero and Ms. This functional Mf would constitute a discrete random variable which can be influenced by a multiplicity of factors, from the degree of motivational arousal and the degree of fatigue to some individual-differences variables."

In the first step of Pascual-Leone`s experimental procedure all subjects learned a small repertoire of stimulus-response units. The number of units to be learned varied across age groups as a function of the predicted maximum M operator size for the group. That it, 5-year-olds learned 5 units, 7-year-olds 6 units, 9-year-olds 7 units, 11-year-olds 8 units. The stimuli forming the repertoire were easily discriminable simple visual cues such as: square, red, dot-inside-the-figure, etc.. The corresponding responses were overlearned motor behaviours such as: raise-the-hand, hit-the-basket, clap-hands, etc.. The universe of simple stimulus-response units used by Pascual-Leone in the whole series of his experiments is presented in Table 1.


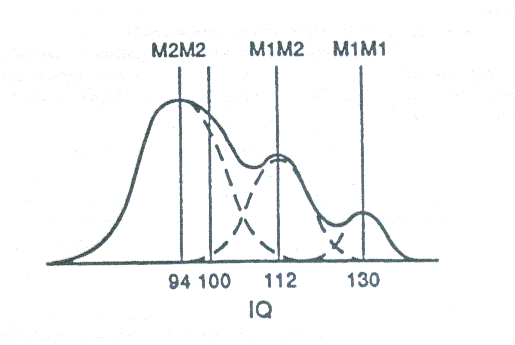
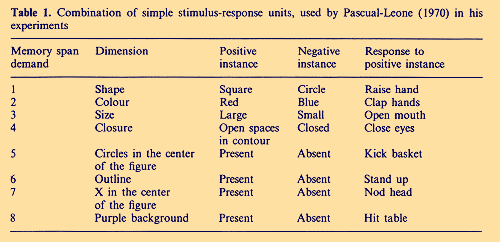Combination of simple stimulus-response units, used by Pascual-Leone (1970) in his experiments

The experimental setting and instructions were as follows: Different sets of cards constituted the stimulus material. Every pair of cards illustrated a simple stimulus-response unit of a given level (see Table 1). Experimenter and subject set facing each other across a table. The task was introduced as a spy game. Experimenter would teach subject a code and when he knew it well, experimenter would send him some secret messages. The whole series was repeated until the subject's motor responses were without error. When the subject had learned his repertoire the second step was introduced. A new randomly ordered set of cards was presented, exhibiting compound stimuli of all possible combinations previously learned by the subject. The subject` s task was to respond to any recognised stimulus. Cards were presented manually and the exposure time was fixed at 5 sec but the subject had free time for responding.

Pascual-Leone`s application (1970; p. 318) of Bose-Einstein statistics to his experimental data seems to be especially remarkable. Because access to chunks in working memory is random, the available energy quanta are not distinguishable. The probability distribution of the random variable x (i.e. the number of different responses produced by the subject) can be calculated on the basis of the combinatorics of the total number c of cues in the stimulus compound (i.e. the span demand of the task; compare Table 1) and the available energy quanta n. By applying the Bose-Einstein occupancy model of combinatorics

Formel (1)
 (1)

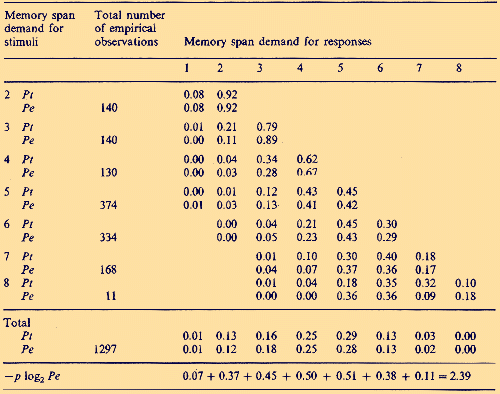
to his learning experiments with children of different age, Pascual-Leone obtained a very good agreement between empirical probabilities Pe (x) and Bose-Einstein predicted theoretical probabilities Pt (x) (see Table 2)

Table 2. Learning experiments by Pascual-Leone (1970, Table6): Bose-Einstein predicted theoretical (Pt) and empirical (Pe) probabilities of compound responses in the sample of 11-year-olds (n=14; experimental observations=1297; mean IQ=119, ranging from 106 to 131; mean age=11.8 years).

As it seems, the deeper meaning of this astounding agreement between a prediction based on a formula of quantum statistics and an outcome of a psychological experiment has never been discussed seriously. But it should. Now we try to extend Pascual-Leone`s theory and results: We have added the last row in Table 2, showing the corresponding -p log2 Pe (x). The information entropy H of a system of indistinguishable particles distributed over occupation number n equals (Yu 1976).

Formel (2)
 (2)

The sum of logarithms to the base 2 of the probabilities that the state n is occupied is 2.39 (see Table 2, last row). For 11-year-olds there are 8 possible quantum states (i.e. the maximum of memory span equals the maximum of such states), hence 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 36.
By multiplying 36 with 2.4 we get for this sample of subjects a mean information entropy H of 86.4 bits. A mean IQ of 119 for 11.8 year-olds corresponds in performance to an adult IQ of 102 for about 40-year-olds. In tables of IQ test results edited by Lehrl et al. (1991) and based on concepts of information theory, we read for this age and IQ 102 a short-term memory storage capacity of 84 bits. Thus, two completely different empirical approaches, one of cognitive psychology the other of differential psychology, with seemingly completely differing theoretical starting points lead on the absolute scale of information entropy to practically the same result. For Pascual-Leone`s data the latter result was even obtained after applying quantum mechanics twice in series, for calculating Bose-Einstein statistics (by Pascual-Leone himself and formula (1)) and information entropy (by formula (2)). To understand the message of all this, we must explain in the following the theoretical background of the so-called Erlangen school (Eysenck 1986, 1987) of information psychology.


3 The Information Entropy of Short-Term Memory Storage Capacity

Shannon`s (1948) information entropy H is the logarithm of the number of microstates consistent with our information. And Thom (1975; p. 157) stated: "To reduce the information to this scalar measure (evaluated in bits of accuracy gained) is to reduce the form to its topological complexity." Each global state of a network can be assigned a single number (Gibbs 1981), called the energy of that state, i.e. the differences in the log probabilities, and hence information entropy of 2 global states ("thoughts") is just their energy difference. By extension of Shannon`s concept of channel capacity, already in 1959 Frank (see Lehrl and Fischer 1990) had claimed cognitive performance to be limited by the channel capacity of short-term memory (Kyllonen and Christal 1990). He argued that the capacity H of short-term memory (measured in bits of information) is the product of the processing speed S of information flow (in bits per second) and the duration time D (in seconds) of information in short-term memory.
Hence

H (bits) = S (bits/s) x D (s) .
(3)


As well known, processing speed can be operationalised in test batteries by sets of elementary cognitive tasks measuring choice reaction time or speed of mental rotation, by scanning information in short-term memory, or by measuring perceptual speed, by testing inspection time or time to escape masking. Such elementary cognitive tasks permit the measurement of individual differences while minimising variance attributable to specific knowledge and acquired intellectual skills and problem-solving strategies. Span and scan are only two sides of the same coin: The greater the memory span, the faster the processing speed. In appropriate samples both variables are perfectly correlated (Cavanagh 1972; Lehrl et al. 1991). - see:

The Basic Period of Individual Mental Speed (BIP)

4 Relationships between EEG Parameters and Psychometric Results

In 1935, Gibbs et al. had already documented that patients (sample size was 55) with petit mal epilepsy show, in all cases during seizures, an outburst of spike waves of great amplitude at a frequency of about 3/s. Now this finding is part of our confirmed knowledge and can be read in every textbook on EEG or epilepsy. From this in 1938, Liberson (see 1985) had drawn the conclusion that all significant channels in EEG could be n multiples of one fundamental frequency of about 3.3 Hz. According to his empirical data the number of these multiples (harmonics) is nine as the maximum of memory span (see Table 1). Assuming these numbers one to nine to be quanta of action (as Pascual-Leone 1970 did), we (Weiss 1986, 1987) obtain a relationship between the classical formulae of quantum statistics and empirical results of both EEG and psychometric research.


Table 3. Memory span (corresponding to the number of an EEG harmonic), frequency of EEG harmonics and mental speed and their relationships with information entropy, power density of short-term memory storage capacity, latencies of harmonics, and IQ (from Weiss, 1992b).
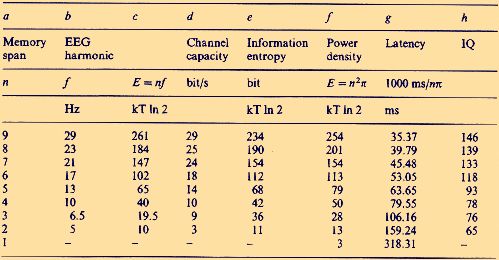
Combination of simple stimulus-response units, used by Pascual-Leone (1970) in his experiments
Column b: empirical data from Liberson (1985). Column c: product of column b times n. Columns a, d, e and h: empirical psychometric data from Lehrl et al. (1991). Their sample size for standardizing the test was 672 subjects. Notice that column e shows empirical data and not the product of column d times n. Columns f and g are purely theoretical. However, Liberson (1985) has published similar empirical latency components of event related potentials.


In order to find a theoretical frame for these connections (see Table 3), we looked (Weiss 1986, 1989) for nearly all applications of wave theory and found especially illuminating textbooks in such fields as geophysics (for example Bath 1974) and optics (Yu 1976). Assuming the numbers 1 to 9 to be harmonics, in accordance with Parseval`s theorem (see Bath, 1974, or any textbook on communication theory) the power spectral density E is given by the eigenstate energy-frequency relationship (see Yu 1976)


E = nf (kT x ln2)
(4)


where f is the frequency. According to thermodynamics, the measurement of 1 bit of information entropy requires a minimum energy of 1 kT x ln2 (Szilard 1929), where k is Boltzmann`s constant and T is absolute temperature. (Of course, this cannot mean that the brain works with this minimum of energy. The relationship, suggested by Table 3, should hold for a macroscopic analogon, whatever it may be; compare Haken 1988). During the duration of 1 perceptual moment 1 bit of information is processed (Lehrl and Fischer 1988) per harmonic. That means that 1 break of symmetry and 1 phase reversal after each zero-crossing of a wave corresponds with a possible 1 bit decision between two alternatives. Consequently, each degree of freedom of oscillation corresponds to a macroscopic analogon of 1 kT, each degree of freedom and translation (this refers to mathematical group theory underlying quantum mechanics; compare Koenderink & Van Doorn, 1990, and Goebel 1990) to an energy of kT/2 or its analogon, respectively. Empirical analysis (Weiss et al. 1986) shows that Liberson`s (1985) fundamental is lower than 3.3 Hz and in the range between 3.1 and 3.3 Hz, i.e. near 3.14 Hz. Therefore, in the following (as in Table 3) we will write for simplification np Hz. Because the frequency of harmonics can be expressed as np Hz, for the expected latencies of harmonics follows 1 000 ms/ np and for power density follows

E = n²p (kT x ln2).

The relationships in Table 1 are further supported by data from Bennett (1972),who reanalysed the Ertl and Schafer (1969) findings of a correlation between IQ and latencies of EEG evoked potential components. Bennett (confirmed by Flinn et al. 1977) accomplished a fourier transformation of the original data and found that high IQ subjects (IQ above 123) go through 20 or more perceptual moments per second, low IQ subjects (IQ below 75) only through 8 moments or even less (compare Table 3, columns b and d). This striking parallelism between EEG results and channel capacity, measured with mental tests, is emphasised by results from Harwood and Naylor (1969). Their subjects were confronted with stimuli of defined information entropy (digits between 1 and 9 and numbers between 1 and 32 presented single or in groups). 42 young university students had a mean channel capacity of 21.4 bit/s; 105 "average normal" adults who were 60-69 years old performed 14.2 bit/s; the age group of 70-79 years (sample size was 67) achieved 12.9 bit/s; and 13 subjects being 80 years and older 10.2 bit/s, thus reflecting the usual decline of mental performance of old aged people. Pure coincidence in this parallelism of channel capacity and EEG frequencies (compare Table 1) seems impossible: neither Liberson nor Lehrl, neither Bennett nor Naylor knew anything about the results and theories of the others.


5 Discussion

The question whether interindivual variations in EEG activity are related to IQ (Gasser et al. 1983) remained always controversial. Because the probability amplitudes of the power spectrum up to 30 Hz depend upon all the memory span of a given individual, upon all its attentional resources, the power in a selected frequency range (for example, in the alpha range) is no good measure for a correlation with IQ. Consequently, the probabilities Pt and Pe (see Table 2) should correspond to the probability amplitudes of the evoked response of a given individual.

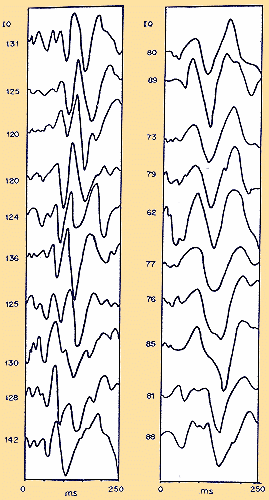
Figure 1

Fig.1 Evoked potential waveforms for ten high and ten low Iq subjects (ertl and Schafer 1069). The individual IQ scores are shown to the left of each waveform. (Note, that only the IQ of individuals is given and not also their respective age. Ertl and Schafer's random sample of 573 primary school purpils comprised grades 2, 3, 4, 5 and 8; and younger children with a given IQ have a lower memory span then older children of the same IQ.)



In 1969 Ertl and Schafer published data on a correlation between IQ and latency components of evoked potentials. Hoewever, some authors could (Perry et al. 1976; Hendrickson and Hendrickson 1980) and many could not replicate their findings or only with substantially lower correlations (for the ongoing discussion see Rothenberger and Meyer-Dittrich 1984; Eysenck 1986; 1987; Weiss 1989). Why? Ertl and Schafer numbered up to 250 ms the peaks and throughs from the left (after stimulation) and they wrote: "The average evoked potentials of the high IQ subjects are more complex, characterized by high frequency components in the first 100 ms which are not observed in the potentials of the low IQ subjects." However, by numbering the peaks from the left, Ertl and Schafer (1969) measured in high IQ subjects latencies of the ninth, seventh, and fifth harmonic. (And the third peak, numbered E4 by Ertl and Schafer, had no real counterpart at all in the waveform of low IQ subjects.) In low IQ subjects positive peaks, caused by higher harmonics, cannot be detected and peaks of the same poststimulus order (and before 250 ms) represent the fifth and third harmonic. (Because the time-reversed fundamental 1000 ms/1p itself, the famous P3OO, is lacking in the Ertl and Schafer data covering only the time range up to 250 ms after stimulus.) However, replicable comparisons of latencies can only be made on the basis of peaks or better zero-crossings which are numbered from the P300 backwards (Haier et al. 1984; Weiss 1989).

When we estimate in Fig. 1 the number of zero-crossings (also denoted as nodes or nodal points) of the waveform (an exact zero-volt-line was not given by Ertl and Schafer), we can easily see that in high IQ subjects this number is about 8, in low IQ subjects about 4 zero-crossings . According to the Wentzel-Brillouin-Kramers (WBK) method of quantum mechanics (Wentzel 1926), the number of zero-crossings (compare Fig. 2) is identical with the quantum number. From this follows: The number of zero-crossings of an evoked potential up to the P300 is identical with memory span (i.e. with the number of macroscopic ordered states).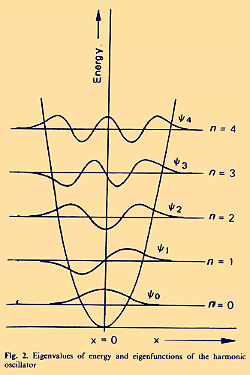
Figure 2 In 1980, Hendrickson and Hendrickson confirmed the correlation between IQ and evoked potential components using the "string" measure. Because the higher IQ subjects have more complex waveforms than the lower IQ subjects "an obvious measure was to think of the waveform as a line. If the line were straigthened out, the more complicated waveform would be longer, and the simple ones would be shorter," for a time range up to the P300. However, is this lenght of the waveform, Hendrickson and Hendrickson's "string" measure, dependent upon something else than the power spectral density of the evoked response?

The physical term power is used because it is a measure of the ability of waves at frequency f to do work. The power spectrum of the EEG describes the total variance in the amplitudes due to the integer multiples of the fundamental frequency. In order to calculate power density in this way, the waveform must be squared and then integrated for the duration of its impulse respone, i.e. the duration of the transient of 1 complete wave packet. Theoretically, the energy E of the impulse response and energy E, given in Table 3, must be identical. What in an evoked response can be found, is not only the response to a given stimulus, a given signal, but also a specific impulse response dependent upon the metabolic mobilisation of brain energy by a given individual. When a stimulus is fed into the brain, the short-term memory wave packet immediately operates on this input, and the result is the corresponding output signal ("a thought"). The mathematical relationship is that the output is equal to the convolution (time reversal) of the input with the short-term memory impulse function (Crick et al. 1981).

Time reversal (the concept of convolution in terms of communication theory) explains, why the higher harmonics occur first after a stimulus. - Surveying data from a very large number of psychophysiological experiments of other authors or published by Geissler himself and coworkers, Geissler (1987, 1990) drew the conclusion that the temporal architecture of mental processes presupposes an universal constant K of approximately 4.5 ms. His theory assumes that all conscious information processing is based on integer multiples of K and chains of multiples as 2K, 3K, 2², 4² and so on (compare also Stroud 1955, who made a similar assumption, based on a secondary analysis of empirical data by Von Bekesy). Multiples as 4, 8, 16, 20, 24, and 28 are preferred.

The Geissler-Stroud-theory has also its counterpart in Table 3. The smallest possible power and time difference, the difference K between the latencies of 9th (35.37 ms) and 8th (39.79 ms) harmonic of the wave packet, is 4.42 ms, itself the 1/72nd part of the fundamental. 9 K is the difference to the 8th harmonic, 12K to the 6th, 18K to the 4th, 24K to the 3rd, 28K to the 2nd. Other important multiples as 3K, 4K, and 10K can easily be identified as differences between harmonics. All higher multiples of K, which are of importance in Geissler`s theory (1990), as 30, 32, 36, and 64 are differences to the 2nd harmonic and the fundamental, respectively. And of course, these higher multiples are themselves cascades of multiples.

What can tell us communication theory on the meaning of such cascades? If ft(t) is a bandlimited signal with a spectrum which is np Hz, then it is determined by its values at the discrete set of points equally spaced at m intervalls of K. Shannon`s sampling theorem (see Jerri 1977) allows the replacement of any continuous signal f(t) by a discrete sequence mK of its samples without the loss of any information. If time divided into equal intervals K ms long and if 1 instantaneous sample is taken from each interval in any manner, then a knowledge of the magnitude of each sample plus a knowledge of the instant at which the sample is taken, contains all the information of the signal. Sample and hold means to take the samples f(mK) from the input signals at the time instants t = mK, and holds them constant by delaying them until the next sampling. The probability of the correct identification of a signal by a wave packet (or wavelet in terms of geophysics, see Kronland-Martinet et al. 1987) is a function of the probability of triggering a determined sequence of frequencies and amplitudes. In other words, the empirical background of the Geissler-Stroud-theory and the relationships of this theory to the results in Table 3, all this is exactly that what would be needed for perfect information processing in terms of communication theory. - It is a pity, that the relationships betwen zero crossings, eigenvalues, and spectral power density (for a review see Robinson 1982), which are common knowledge in information technology (Jerri 1977), are virtually unknown in cognitive psychology and neurophysiology. Because it is impossible in the context of such an article, to repeate a large number of formulae and proofs, we must refer again to the above mentioned textbook (Resnikoff 1989) as an obligatory background to understand our following summarising: The most extreme compression of information is represented by the eigenvalues (Kac 1966) of the spectrum. These eigenvalues are always multiples of K. Their knowledge allows to transmit and to reproduce any information. There are as much eigenvalues of a spectrum as are harmonics (Wentzel 1926; see Fig. 2). Each eigenvalue of event related electrocortical potentials is represented by a zero-crossing up to the P300 (Weiss 1989).

In view of the fact, that to the Soviet Livanov-school of psychophysiology (see Lebedev 1990) the correlation between EEG parameters and memory span (Polich et al. 1983) was well known for at least a decade, it is surprising that this identity between memory span and the number of zero- crossings has not been seen earlier. That the number of zero-crossings of an epoch of the EEG up to about 300 ms represents its power spectral density, was already known to Saltzberg and Burch (see 1971) in 1959. However, these EEG results were nearly forgotten before the advent of a new brand of signal detection theory, stressing the importance of zero-crossings (Niederjohn et al. 1987; Zeevi et al. 1987; Yuille and Poggio 1988).

Johnson (1988) stated that overall P300 amplitude represents the summation of effects due to two independent variables: subjective probability (P) and stimulus meaning (M). The amplitude attributable to each of these two dimensions depends on the proportion (T) of the overall stimulus information which was transmitted to the subject. Thus:

P300 amplitude = f ( T x (1/P + M ))
(6)


This attempt, to explain the contribution of P300 to spectral density in terms of information theory, has with our explanation in common that the three dimensions (Johnson 1988) contain inherently the same subjective (IQ) and objective (amount of information measured in bits) elements as our approach, plus the information entropy of the stimulus itself. We hope, that the intinuitive appeal of this underlying congruency will be such a strong one that the two approaches can be reconciled by future research into one formula and one coherent theory of event-related potentials.

This article tries to summarise well-established empirical facts and theoretical conclusions and to avoid speculations. Therefore, it seems not premature (compare also Basar 1988) to conclude: In analogy to quantum mechanics the brain seems to be an ideal detector simply measuring the energy of wave formes. No matter what the stimulus is and how the brain behaves, the metric of signal and memory can always be understood as a superposition of wave packets of np states of different energy and their eigenvalues. Time is the currency (compare Jones 1976), interconverting energy, information, and spatial distance (Weiss 1990).

References
  • Basar E (ed) (1988)
    Dynamics of sensory and cognitive processing by the brain Springer, Berlin
  • Bath M (1974)
    Spectral analysis in geophysics. Elsevier, Amsterdam
  • Bennett WF (1974)
    The fourier transform of evoked responses. Nature 239: 407-408
  • Cavanagh JP (1972)
    Relation between the immediate memory span and the memory search rate. Psychol Rev 79:525-530
  • Crick FHC, Marr DC, Poggio T (1981).
    An information-processing approach to understanding the visual cortex. In: Schmitt FO, Worden EG, Edelman G, Dennis C (eds.). The organization of the cerebral cortex. MIT Press, Cambridge, pp 505-535
  • Ertl JP, Schafer EWP (1969)
    Brain response correlate of psychometric intelligence. Nature 223:421-422
  • Eysenck HJ (1986)
    The theory of intelligence and the psychophysiology of cognition. In: Sternberg RJ (ed) Advances in the psychology of human intelligence. Vol. 3. Erlbaum, Hillsdale NJ, pp 1-34
  • Eysenck HJ (1987)
    Speed of information processing, reaction time, and the theory of intelligence. In: Vernon PA (ed). Speed of information-processing and intelligence. Ablex, Norwood, pp 21-68
  • Flinn JM, Kirsch AD, Flinn EA (1977)
    Correlations between intelligence and the frequency content of the evoked potential. Physiol Psychol 5:11-15
  • Fogleman G (1987)
    Quantum strings. Am J Phys 55:330-336
  • Gasser T, Von Lucadou I, Verleger R, Bächer P (1983)
    Correlating EEG and IQ: a new look at an old problem using computerized EEG parameters. Electroenceph Clin Neurophysiol 55:493-504
  • Geissler H-G (1987)
    The temporal architecture of central information processing: evidence for a tentative time-quantum model. Psychol Res 49:99-106
  • Geissler H-G (1990)
    Foundations of quantized processing. In: Geissler H-G (ed) Psychophysical explorations of mental structures. Hogrefe and Huber, Toronto, pp 193-210
  • Gibbs FA, Davis H, Lennox WG (1935)
    The electroencephalogram in epilepsy and in conditions of impaired consciousness. Arch Neurol Psychiat (Chic) 34: 1133-1148
  • Gibbs WR (1981)
    The eigenvalues of a deterministic neural net. Math Biosc 57:19-34
  • Goebel PR (1990)
    The mathematics of mental rotations. J Math Psychol 34:435-444
  • Haken H (1988)
    Information and self-organization: a macroscopic approach to complex systems. Springer, Berlin
  • Haier RJ, Robinson DL, Braden W (1984)
    Electrical potentials of the cerebral cortex and psychometric intelligence. Person individ Diff 4:591-599
  • Harwood E, Naylor GFK (1969)
    Rates of information transfer in elderly subjects. Austr J Psychol 21:127-136
  • Hendrickson DA, Hendrickson AE (1980) The biological basis of individual differences in intelligence. Person individ Diff 1:3-33
  • Jerri AJ (1977)
    The Shannon sampling theorem - its various extensions and applications: a tutorial review.Proc IEEE 65:1565-1596
  • Johnson R (1988)
    The amplitude of the P300 component of the event-related potential: review and synthesis. Adv Psychophysiol 3:69-137
  • Jones MR (1976) Time, our lost dimension: toward a new theory of perception, attention and memory. Psychol Rev 83:323-355
  • Kac M (1966)
    Can one hear the shape of a drum? Am Math Monthly 73, part II:1-23
  • Koenderink JJ, Van Doorn AJ (1990)
    Receptive field families. Biol Cybern 63:291-297
  • Kronland-Martinet R, Morlet J, Grossmann A (1987)
    Analysis of sound patterns through wavelet transforms. Internat J Pattern Recogn Artific Intell 1:273-302
  • Kyllonen PC, Christal RE (1990)
  • Reasoning ability is (little more than) working memory capacity. Intelligence, 14, 389-433.
  • Lebedev AN (1990)
    Cyclic neural codes of human memory and some quantitative regularitities in experimental psychology. In: Geissler H-G (ed) Psychophysical explorations of mental structures. Hogrefe and Huber, Toronto, pp 303-310
  • Lehrl S, Fischer B (1988)
    The basic parameters of human information processing: their role in the determination of intelligence. Person individ Diff 9:883-896
  • Lehrl S, Fischer B (1990)
    A basic information psychological parameter for reconstruction of concepts of intelligence (BIP). Eur J Person 4:259-286 - see: The Basic Period of Individual Mental Speed (BIP)
  • Lehrl S, Gallwitz A, Blaha L, Fischer B (1991)
    Geistige Leistungsfähigkeit. Theorie und Messung der biologischen Intelligenz mit dem Kurztest KAI. Vless, Ebersberg
  • Liberson WT (1985)
    Regional spectral analysis of EEG and 'active' and 'passive' intelligence. In : Giannitrapani D. The electrophysiology of intellectual functions. Karger, Basel, pp 153-176
  • Miller GA (1956)
    The magical number seven, plus or minus two: some limits on our capacity for processing information. Psychol Rev 63:81-97
  • Niederjohn RJ, Krutz MW, Brown BM (1987)
    An experimental investigation of the perceptual effects of altering the zero-crossings of a speech signal. IEEE Trans Acoust Speech Signal Processing 35:618-625
  • Pascual-Leone J (1970)
    A mathematical model for the transition in Piagetian developmental stages. Acta Psychol 32:301-345
  • Penrose R (1990)
    The emperor` s new mind - concerning computers, minds, and the laws of physics. Behav Brain Sci 13:643-706
  • Perry NW, Jr, McCoy JG, Cunningham WR, Falgout JC, Street WJ (1976)
    Multivariate visual evoked response correlates of intelligence. Psychophysiol 13:323-329
  • Piaget J (1971)
    The theory of stages in cognitive development. In: Green ED
    (ed) Measurement and Piaget. Mc Graw Hill, New York, pp 1-11
  • Polich J, Howard L, Starr A (1983)
    P300 latency correlates with digit span. Psychophysiol 20:665-669
  • Resnikoff HL (1989)
    The illusion of reality. Springer, New York.
  • Robinson EA (1982)
    A historical perspective of spectrum estimation. Proc IEEE 70:885-907
  • Rothenberger A, Meyer-Dittrich M (1984)
    Beziehungen zwischen elektrischer Hirnaktivität und Intelligenz im Kindesalter. Z Kinder- Jugendpsychiatr 12:79-104
  • Saltzberg B, Burch NR (1971)
    Period analytic estimates of the power spectrum: a simplified EEG domain procedure. Electroenceph Clin Neurophysiol 30:568-570
  • Shannon CE (1948)
    A mathematical theory of communication. Bell System Technol J 27:379-432 and 623-656
  • Stroud JM (1988)
    The fine structure of psychological time. In: Quastler H.
    (ed) Information theory in psychology. Free Press, Glencoe, pp 174-207
  • Szilard L (1929)
    Über die Entropieverminderung in einem thermodynamischen System bei Eingriff intelligenter Wesen. Z Physik 53:840-856
  • Thom R (1975)
    Structural stability and morphogenesis. Benjamin Cummings, Reading, MA
  • Vichnevetsky R (1988)
    Quantum properties of wave propagation in periodic structures. Syst Anal Model Simul 5:103-129
  • Weiss V (1986)
    From memory span and mental speed toward the quantum mechanics of intelligence. Person individ Diff 7:737-749
  • Weiss V (1987)
    The quantum mechanics of EEG-brain dynamics and short-term memory. Biol Zentralblatt 106:401-408
  • Weiss V (1989)
    From short-term memory capacity toward the EEG resonance code. Person individ Diff 10:501-508
  • Weiss V (1990)
    The spatial metric of brain underlying the temporal metric of EEG and thought. Gegenbaurs morphol Jahrb 136:79-87
  • Weiss V, Lehrl S, Frank HG (1986)
    Psychogenetik der Intelligenz. Modernes Lernen, Dortmund.
  • Wentzel G. (1926)
    Eine Verallgemeinerung der Quantenbedingungen für die Zwecke der Wellenmechanik. Z Physik 38:518-529
  • Yu FTS (1976)
    Optics and information theory. Wiley, New York.
  • Yuille AL, Poggio TA (1988)
    Scaling and fingerprint theorems for zero crossings. Adv Comp Vision 2:47-78
  • Zeevi YY, Gavriely A, Shamai S (1987)
    Image representation by zero and sine-wave crossings. J Opt Soc Am A 4:2045-2060

    Home

    The golden mean as clock cycle, the powers of the golden mean and the golden mean shift as coding principle of the brain

    Harald Weiss and Volkmar Weiss

    Preliminary communication on an invited talk, held by Volkmar Weiss at the 5th Sommerfeld-Seminar 2002 of the Arnold-Sommerfeld-Society, University of Leipzig, Neuer Senatssaal, May 16th, 2002, 17 pm

    At first, Weiss recapitulated the empirical findings and theoretical conclusions of two already published  papers (see www.volkmar-weiss.de/publ10-e.html and www.volkmar-weiss.de/publ9-e.html , also available on the server of Stanford University, see http://www.slac.stanford.edu/~terryh/01Books/010Human-Paradigm/390Intelligence-IQ/030IQ-WM.html  and http://www.slac.stanford.edu/~terryh/01Books/010Human-Paradigm/390Intelligence-IQ/020IQ-Brain-Energy.html

    With one decisive difference: Where you are reading Pi (3,14) in these papers, you should read 2 Phi (3,236). (Without reading and understanding of these two papers, the following new conclusions have no sense at all.) Some colleagues complained that they could not open the above mentioned URLs. I thought it would be already common knowledge: In order to open such an URL, at first you have to write http://www.slac.stanford.edu/, than add http://www.slac.stanford.edu/~terryh/ and click through the directory of Terryh in the order given above, 01Books/ followed by 010Human-Paradigm/ and so on or add it manually step by step. Or try it with the support of http://www.google.com/ , filling in the URL in the same manner, step by step.

    We have the crucial question to answer: Why is the clock cycle of the brain 2 Phi and not 1 Phi? What is the advantage of the fundamental harmonic to be 2 Phi? Half of the wavelength of 2 Phi , that means 1 Phi and its multiples are exactly the points of resonance, corresponding to the eigenvalues and zero-crossings of the wave packet (wavelet). With this property the brain can use simultaneously the powers of the golden mean and the Fibonacci word for coding and classifying. Compare, for example,  http://arxiv.org/pdf/cond-mat/9505072 and http://arxiv.org/pdf/cond-mat/9505072. A binomial graph of a memory span n has n distinct eigenvalues and these are powers of the golden mean. The number of closed walks of length k in the binomial graph is equal to the nth power oft the (k+1)-st Fibonacci number. The total number of closed walks of length k within memory is the nth power of the kth Lucas number. See Peter R. Christopher http://users.wpi.edu/~bservat/symsch97.html

    An extended publication, summarising  the arguments in favour of this new interpretation of the data - i.e. 2 Phi instead of Pi - is in preparation. In order to accelerate the discussion, in the following the most important links are given why Phi (the golden mean, synonymously called the golden section, the golden ratio, or the divine proportion), the integer powers of Phi, the golden rectangle, and the infinite Fibonacci word 10110101101101 … (FW, synonymously also called the golden string, the golden sequence, or the rabbit sequence) are at the root of the information processing capabilities of our brains.

    Links:

    Cited from: http://home.earthlink.net/~sroof/Abraxas/sar/phi/phi.htm, Period Doubling Route to Chaos:  It turns out when R = 2 Phi = 2 times 1,1618 =  3,236 one gets a super-stable period with two orbits. What this means is that Phi enters into non-linear process as the rate parameter which produces the first island of stability.

    The same holds for the Feigenbaum constants, the length w1 is positioned at a = 2 Phi, see http://pauillac.inria.fr/algo/bsolve/constant/gold/gold.html  .  See also: bifurcation, logistic parabola equation, edge of chaos. http://www.rootnode.com/Wiki/ProjectLab/LogisticMap
     

    The most important link is the Fibonacci Homepage. See especially the four chapters Phi and the Rabbit sequence (= FW) and The rabbit sequence (= FW) and the spectrum of Phi and Phi’s fascinating figures (integer powers of Phi) and Integers as sums of powers of Phi) http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibrab.html

    http://www.geocities.com/CapeCanaveral/Launchpad/5577/musings/Attractors.html

    The following property of the FW is already applied in image processing and recognition of handwriting:

    The Phi line Graph

    If we draw the line y = Phi x on a graph, (ie a line whose gradient is Phi) then we can see the Fibonacci word directly.

    Where the Phi line crosses a horizontal grid line (y=1, y=2, etc) we write 1 by it on the line and where the Phi line crosses a vertical grid line (x=1, x=2, etc) we record a 0.

    Now as we travel along the Phi line from the origin, we meet a sequence of 1s and 0s - the Fibonacci sequence again!

    1 0 1 1 0 1 0 1 1 0 1 1 0 1 0 1 1 0 1 0 1 1 0 1 1 0 1 0 1 1 0 1 ...

    The frequency of occurrence of either 1 or 0 is called the sampling frequency by engineers.
      

    Of fundamental importance: The Fibonacci word and the spectrum of Phi

    Let's look  at the multiples of Phi,  concentrating on the whole number part of the multiples of Phi. We will find another extraordinary relationship.
    The "whole number part" of x is written as floor(x) so we are looking at floor(i Phi) for i=1,2,3,.. .
    In this section on the Fibonacci word will only be interested in positive numbers, so the floor function is the same as the trunc function.

    The sequence of truncated multiples of a real number R is called the spectrum of R.

    Here are the first few numbers of the spectrum of Phi, that is the values of the Beatty sequence floor(Phi), floor(2 Phi), floor(3 Phi), floor(4 Phi), ..:- (Compare http://mathworld.wolfram.com/BeattySequence.html )

    i

    1

    2

    3

    4

    5

    6

    7

    8

    ...

    i Phi

    1.618

    3.236

    4.854

    6.472

    8.090

    9.708

    11.326

    12.944

    ...

    trunc(i*Phi)

    1

    3

    4

    6

    8

    9

    11

    12

    ...

    So the spectrum of Phi is the infinite series of numbers beginning 1, 3, 4, 6, 8, 9, 11, 12, ... .

    Now look at the Fibonacci sequence and in particular at where the 1s occur:

    I

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    13

    ...

    Fibonacci word

    1

    0

    1

    1

    0

    1

    0

    1

    1

    0

    1

    1

    0

    ...

    This pattern is true in general and provides another way of defining the Fibonacci word:

    The 1s in the Fibonacci word occur at
    positions given by the spectrum of Phi
    and only at those positions.

    There is also a remarkable relationship between the spectrum of a number and those numbers missing from the spectrum.

    Our brain uses for computing inherent and inborn properties of the physical world.  We have or learn into the neural network of our brains the relationships between external stimuli, the integer powers of the golden mean, the Fibonacci word and Lucas numbers, the Beatty sequences of e, Pi, Phi and use hundreds of similar relationships (many of them maybe still undiscovered by contemporary mathematics) between numbers for encoding and decoding simultaneously and unconsciously by wavelets. Only a genius like Ramanajun had some access to this underlying world of numbers. For example, he gave us: Phi (2) = 2 ln2, Phi (3) = ln3, Phi(4) = 3/2 ln2, Phi(5) = 1/5 root of 5 lnPhi + ½ ln5, Phi(6) = ½ ln3 + 2/3 ln2. See http://mathworld.wolfram.com/RamanujanFunction.html 

    Cited from: http://www.washingtonart.net/whealton/fibword.html  A sub-word of the FW is any fragment such as "abab" (or written 1010 as above) or "baa" (or 011). Certain patterns occur as observable sub-words of the FW "a," "b," "aa," "ab," "ba," etc., and certain conceivable patterns do not.. At length one, two fragments are theoretically possible, "a," and "b." Both of them actually occur. At length two, the theoretically possibilities are "aa," "ab," "ba," and "bb." Here, the last one is never present, as we have seen. At length three, only four of the eight possible patterns occur. They are "aab," "aba," "baa," and "bab." At length four, only five of the sixteen possible patterns actually occur. At length five, only six out of the thirty-two theoretically possible patterns are seen. In fact, whatever the length of sub-word that is examined, it is always found that the number of distinct sub-words actually occurring of that length in the FW is always one more than the length itself. The probability of finding a subword (and its parent or progeny, see the following) of a wave packet with a maximum of up to nine harmonics can be calculated by hidden Markov chains.

    One pattern over another is the simple act of one pattern generating another, as "abaab" generates "abaab" or even as sub-word "bab" generates "aaba." At length 1, two legal sub-words are found, "a" and "b." At length 2, three legal sub-words are found, "aa," "ab," and "ba." Here is where the new notion of descent comes in. One can think of "aa" and "ab" as children of parent "a" because both "aa" and "ab" can be created by appending a letter after the pattern, "a". By the same logic, pattern "ba" has parent pattern, "b." Continuing, one sees that "aa" is parent of "aab," that "ab" is parent of "aba," and that "ba" is parent of both "baa" and "bab." Simple arithmetic suggests that all but one of the sub-words of any given length will act as parent for a single sub-word of length one letter larger, while one sub-word alone will give birth to two progeny. No other pattern is possible, for all sub-words must have at least one child.
    Moving from length three to length four, we note that "aab" produces "aaba," that "aba" gives rise to "abaa," as well as to "abab, and that "baa" sires "baab," At the next level, "aaba" produces "aabaa" and "aabab," "abaa" gives "abaab," "abab" gives "ababa," and "baab" gives "baaba," and "baba" gives "babaa."

    It turns out that the hyperparental sub-word, at any given length, is precisely the FW itself of that length, written in reverse order. That means that the FW reproduces itself upon reverse mapping (also called block renaming or deflation in renormalization theories in physics). This is the basic coding and search principle of information in our brain. According with Zipf's law the most common and short words have the highest probability of immediate access, rare words a low probability. The coding itself needs learning. Only the principle is the same, the details and content differ between individuals.

    The best introduction into FW properties in this context you find in: Schroeder, Manfred: Fractals, Chaos, Power Laws. New York: W. H. Freeman 1991, pp. 45-57 and pp. 304ff.

    The most comprehensive book for the physical implications of the golden mean is: de Spinadel, Vera W.: From the Golden Mean to Chaos. Vicente López 1998. (The book is still available, ISBN 950-43.9329-1)

    Image processing, the FW as the reference pattern for coding, see, for example, http://members.aol.com/kwpapke/GoldenDots.html

    For computer science the FW is no newcomer. Processing of strings of symbols is the most fundamental and the most common form of computer processing: every computer instruction is a string, and every piece of data processed by these instructions is a string. Combinatorics of words is the study of arrangement of such strings, and there are literally thousands of combinatorial problems that arise in computer science. You will find the relevant links and hundreds of papers and books of the research front, if you feed into the searching robot of Google: string, Sturmian, Fibonacci, combinatorics of words, code, golden mean, string rewriting and combinations of these concepts. See, for example http://www.infres.enst.fr/~jsaka/PUB/FibGoldResume.html

    Examples of further links:

    A self-generating set and the golden mean http://www.research.att.com/~njas/sequences/JIS/VOL3/goldentext.html, see also the One-Line Encyclopedia of Integer Sequences A005614, A003849 by N.J.A.Sloane.

    Scaling  behavior of entropy estimates, see http://www.geocities.com/ts271/schuermann-02.pdf 

    The mathematical background behind al these relationships, of course, is the prime number distribution, Ulam spiral, Pascal's triangle and so on, for a summary of related links see http://www.maths.ex.ac.uk/~mwatkins and http://www.maths.ex.ac.uk/~mwatkins/zeta/ulam.htm .The most essential formulas are from Ramanujan where Pi, e and Phi are closed-form expressions of infinite continued fractions, all three together united in one such formula.

    In mathematics Cantorian fractal space-time is now associated with reference to quantum systems. Recent studies indicate a close association between number theory in mathematics, chaotic orbits of excited quantum systems and the golden mean. See, for example, http://xxx.lanl.gov/html/physics/0005067 and http://xxx.lanl.gov/abs/hep-th/0203086  and http://xxx.lanl.gov/abs/hep-th/0203086 for prime powers of the golden mean  also http://www.liafa.jussieu.fr/~cf/publications/fibgold.ps  , for the spatial entropy two dimensional golden mean see http://www.math.nctu.edu.tw/People/e_faculty/jjuang.htm

    Further links are available, following http://mathworld.com/RabbitSequence.html and http://www.worldofnumbers.com/won118.htm

    Prof. Oleksiy Stakhov has dedicated his life to the role of the golden section as a code, see http://www.uem.mz/faculdades/ciencias/informat/docentes/stakhov/cont.htm

    Fibonacci L-sytems  http://www.math.okstate.edu/mathdept/dynamics/lecnotes/node59.html

    Golden mean frequency, golden mean scaling, period two orbit, renormalization, binary search tree, Fibonacci shuffle tree, digital search tree, Feigenbaum-Shenker scaling constant, 2d Golden mean or Hard square model, golden mean renormalisation of the Harper equation, bit-string physics

    http://www.maths.ex.ac.uk/~bdm/additive_indep.pdf

    http://www.math.hut.fi/~kve/resgraph.html

    http://www.lboro.ac.uk(departments/ma/preprints/papers00/00-7.pdf

    The golden mean in quantum geometry, knot theory and related topics http://www.ams.org/mathscinet-getitem?mr=2000c:11213

    A speculative paper by Nigel Reading, but hinting in the right direction http://geocities.com/Area51/Starship/9201/phimega/phimega.html

    Sturmian sequences, entropy understood as pattern matching (see also the 1994 Shannon lecture by Aaron D. Wayner) http://math.washington.edu/~hillman/PUB/Fibonacci and http://www-ext.crc.ca/fec/golden_Ref5.pdf

    Optimal search strategy of bees: a lognormal expanding spiral, based on the golden section, fits the data best http://www.beesource.com/pov/wenner/az1991.htm. This behaviour can be generalized to an optimal search strategy, for example, for searching words in long-term memory (Zipf's law) or filtering information from images. There are applications by Chaitin and others.

    It is an astounding psychoacoustic fact, known as octave equivalence that all known musical cultures consider a tone twice the frequency of another to be, in some sense, the same tone as the other (only higher). On the background of such observations Robert B. Glassman wrote his review: "Hypothesized neural dynamics of working memory: Several chunks might be marked simultaneously by harmonic frequencies within an octave band of brain waves". See http://www.geocities.com/ripps/glassman.pdf  Glassman's review is essentially congruent with the papers by V. Weiss.  We assume that behind octave equivalence is the relation between 2 Phi and 1 Phi, too.

    As you can see, the idea that the Fibonacci word can be understood or can be used as a code, is not a new one. There are already a lot of applications. However, new (by neglecting a lot of nonsense with quasi-religious appeal) is the claim, supported by proven empirical facts of psychology and neurophysiology, that our brain uses the golden mean as the clock cycle of thinking and hence the powers of the golden mean and the FW as principle of coding.

    In 1944 Oswald Avery discovered that DNA is the active principle of inheritance. It lasted still decades before the genetic code was known in detail and six decades later the human genome was decoded. It will last some decades more, to understand the network of genetic effects in its living environment. We believe that our discovery of the fundamental harmonic of the clock cycle of the brain can be compared with Avery's achievement.

    In 1986 the senior author (V.W.) exchanged papers and letters with a young man: Stephen Wolfram. One reason, why we do no present a full paper now, is the expectation raised by his book "A New Kind of Science". We are eager to read this book before we write an extended new publication of our own.  Today, May 17th, the book is still not available in Germany.

    The authors:  Harald Weiss (Nuremberg), born in 1971, Dip. engineer of information technology; PD Dr. Dr. habil. Volkmar Weiss (Leipzig), born in 1944.

    Home