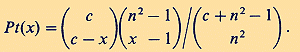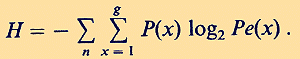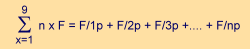
Home
other publications
German Central Office for Genealogy
Die IQ-Falle
E-Mail
Last update 10/2008
|
The IQ-Trapper |
| Where you are reading Pi (3,14) in the following paper from 1995, you should replace Pi by 2 Phi (3,236) -
see: Weiss, Harald and Volkmar Weiss: The golden mean as clock cycle of brain waves. Chaos, Solitons and Fractals, Volume 18 , Issue 4, Pages 643-652 (November 2003) - Elsevier Author Gateway, online version - Short term memory capacity, Attention, EEG, Quantum mechanics of intelligence
Memory Span as the Quantum of Action of Thought
Abstract. NeoPiagetians have claimed memory span to be the missing link between psychometrically defined intelligence and cognition, i.e. span to be the most important human limitation in reasoning and problem solving. Changes in children`s logical abilities are contingent upon a maturational increase of memory span. In research done by Pascual-Leone the maximum of memory span became the mental energy operator. By applying the Bose-Einstein-occupancy model of quantum statistics to learning experiments, Pascual-Leone obtained a very good agreement between empirical findings and Bose-Einstein predicted probabilities. Multiplying memory span by mental speed (bits processed per unit time), operationally defined as reading rate, and using the entropy formula for indistinguishable quantum particles (bosons), the so-called Erlangen school of information psychology calculates short-term memory storage capacity and obtains numerically by IQ testing the same result as Pascual-Leone by learning tests. If we understand memory span as the quantum number of a harmonic oscillator, we have a third way to get even this same result from evoked potentials of the EEG, now in terms of power spectral density of the EEG.VOLKMAR WEISS Key words: Short-term memory storage capacity, neoPiagetian, cognitive development, IQ, processing speed, reading rate, power spectral density of the EEG. INTRODUCTION Ever since attention became the object of scientific study, psychologists have recognised that it possesses a quantitative dimension in terms of the maximum number of items to which a person can attend at one time. Attempts to measure this span of attention revealed that it was indeed limited, but that those limits were fluid and depended on a variety of factors. However, the discovery of a constant in science, even a "fuzzy" one, is an important event. A case in point is Miller`s (1956) number seven plus or minus two. It now seems almost universally accepted that short-term memory has a capacity limit of around this value. The possibility that such quantitative limits on attention span might be related to qualitative differences in thought and reasoning was recognised by Piaget (see 1971) in his earliest research reports. In some passages, he suggested that increases in attention span took a leading role with respect to cognitive development insofar as the logical form of children`s reasoning was "conditioned" by the breadth of their fields of attention. Although his writings contain repeated references for the role of span or "field" of attention in cognitive development, his interest was always focused on qualitative developmental changes. The advent of cognitive psychology and information processing theories provided a new stimulus for theories regarding the nature and consequences of limitations in attention capacity. Although such limits were often located in "short-term memory" or "working memory", a close relation between memory and attention was recognised in many models of human information processing. The possibility that such processing limitations might constrain human reasoning and problem solving was acknowledged by several authors (Bjork, 1975; Bachelder & Denny, 1977; Dempster, 1981; Chapman, 1990; Kyllonen & Christal, 1990; Just & Carpenter, 1992; Cantor & Engle, 1993; Jensen, 1993; Morra, 1994). A thorough analytic understanding of the nature of memory span would probably constitute a major step toward understanding psychometric intelligence (Andres Pueyo, 1993), too. If a sound understanding of memory span performance cannot be achieved, it is unlikely that a sound understanding of performance in more complex tasks can be achieved. However, until now there is no general agreement among theorists that short-term memory is the workspace of thinking, or that span tests measure processing capacity (see for a review of the counterarguments, Halford, Maybery, O`Hare, & Grant, 1994). For example, Baddeley and Hitch (1974) argue for the existence of a central executive and a set of slave storage systems, such as an articulatory loop and a visuo-spatial scratch pad. According to the earlist statement of this model, the central executive is a general-purpose workspace which can be allocated to both information processing and temporary information storage (compare Hitch, Halliday, & Littler, 1989). In terms of the Baddeley and Hitch (1974) working memory model, the following can be understood as a contribution to the theory of the central executive as a general-purpose limited-capacity system. THE COMMON DENOMINATOR OF COGNITIVE AND OF INFORMATION PSYCHOLOGY Beginning with Pascual-Leone (1970), the prediction of children`s reasoning from estimates of their memory span has been a major goal of neoPiagetian theories of cognitive development. A common feature of these theories is the proposition that the growth of memory span is a causal factor in the development of children`s reasoning (de Ribaupierre et al., 1989; Morra, 1994), such that a certain level of capacity is necessary but not sufficient for a given level of reasoning. Although substantial evidence exists to support a general dependency of reasoning upon short-term memory capacity (see Case, 1985; Halford et al., 1994), the above-mentioned theories differ with respect to (a) nature of the capacity construct, (b) the ways in which units of capacity are defined and measured, and (c) the specific relations of correspondence between units of capacity and stages or levels of cognitive development (see for a comparative review, Chapman, 1990). In the following we will restrict our analysis to findings published by Pascual-Leone (1970), who himself reported (Pascual-Leone, 1987, p. 534): "In 1963 I proposed to Piaget the concept of mental capacity, or mental-attention mechanism, capable of boosting a limited number of schemes to ensure their control of the subjects performance. In situations where the task-relevant schemes are not strong, because other irrelevant schemes are boosted by perceptual factors ... , I saw the inevitability of cognitive conflicts between task-relevant schemes and irrelevant ones. ... This outcome was unavoidable in theory unless an organismic factor exists capable of boosting relevant schemes whenever they are weaker. This was to be the function of my mental attentional capacity. There were precursors in psychology for this kind of model: Spearman`s mental energy/ g-factor or ... Luria`s energy level of the central nervous system. ... Piaget understood very well this idea of a mental capacity but did not like it. He could not see how a quantitative construct could possibly explain the many compelling qualitative differences found in mental processing from infants to preschoolers, to schoolers, to high-schoolers. He was a purely qualitative theorist in the classic scientific sense, with a keen interest in logical analysis and logical descriptive modelling, but little sensitivity towards the real-time analysis of task situations." In a typical Piagetian class inclusion task, children are shown a collection of objects (e.g. wooden beads), most of which are of one colour (e.g., red) and the rest of another colour (e.g., white). Children are asked if there are more red beads or more wooden beads and are credited with class inclusion if they indicate that there are more wooden beads because the red beads are included in the total class of wooden beads. According to Piaget (1971), class inclusion is characterised by an operation of class addition having the form A + A` = B, where A represents a subclass of objects defined by a particular property (e.g., the red beads), B represents the supraordinate class defined by some other property (the wooden beads), and A` is the complement of A under B (the wooden beads are not red). Understanding class inclusion thus implies understanding that a supraordinate class (B) is necessarily equivalent to the sum of its subclasses (A and A`). With respect to the capacity requirements of class inclusion, the important thing is that all three class variables, A, A` and B, must be assigned values simultaneously. Under the assumption that each simultaneous value assignment requires a "unit" of capacity, the operation of class addition would require a minimum of 3 such units, that means a memory span of 3. It was shown by Humphreys, Rich, & Davey (1985) that a total score on 27 Piagetian tasks was very highly correlated (r = .88) with the 14-item Wechsler IQ test. From only 13 Piagetian tasks Humphreys et. al. could form a test that is an excellent measure of general intelligence in its own right but can also add to the information furnished by Wechsler Verbal and Performance IQs and academic achievement. This should be no surprise, because more sophisticated Piagetian tasks and many IQ subtests have much in common. For example, in a Piagetian task assessing the multiplication of classes and the multiplication of relations, children were shown 2 x 2 matrices in which three of the four cells were filled with objects. In each case, they were asked to fill in the missing cell with an object that completed the matrix. In the multiplication of classes task, the rows of the matrix were defined by classes of objects differing in shape, and the colums by classes differing in colour. In the multiplication of relations task, the rows and colums were defined by relations of shape and size, respectively. By combination of criteria defining different classes, a given task will be more and more difficult (Scardamalia, 1977) and more memory span will be required. Piagetian tasks and ordinary IQ test item differ only that in Piagetian tasks this minimum of memory span to solve the task is known, in ordinary tests not or not explicitly. In the pioneering research by Pascual-Leone (1970) the maximum of memory span became the mental energy operator M (compare Morra, 1994). Maximum mental power (= M) is characterised as the maximum absolute number of different schemes (including overlearned complex subroutines and strategies) that can be activated in a single mental act. Pascual-Leone (1970; p. 304) understands memory span as the maximum of discrete and equal energy units (i.e. quanta) which every subject has at his disposal. "Assuming that M operates upon the units or behavioural segments available in the subject`s repertoire, as the repertoire changes with learning so will the level of performance even if the subject`s M value remains constant. A distinction can and should be made between the subject`s maximum capacity or structural M (Ms) and his functional M (Mf) or amount of Ms space actually used by him at any particular moment of his cognitive activity. It seems reasonable to assume that the value taken by Mf oscillates between zero and Ms. This functional Mf would constitute a discrete random variable which can be influenced by a multiplicity of factors, from the degree of motivational arousal and the degree of fatigue to some individual-differences variables." In the first step of Pascual-Leone`s experimental procedure all subjects learned a small repertoire of stimulus-response units. The number of units to be learned varied across age groups as a function of the predicted maximum M operator size for the group. That it, 5-year-olds learned 5 units, 7-year-olds 6 units, 9-year-olds 7 units, 11-year-olds 8 units. The stimuli forming the repertoire were easily discriminable simple visual cues such as: square, red, dot-inside-the-figure, etc.. The corresponding responses were overlearned motor behaviours such as: raise-the-hand, hit-the-basket, clap- hands, etc.. The universe of simple stimulus-response units used by Pascual-Leone in the whole series of his experiments is presented in Table 1. 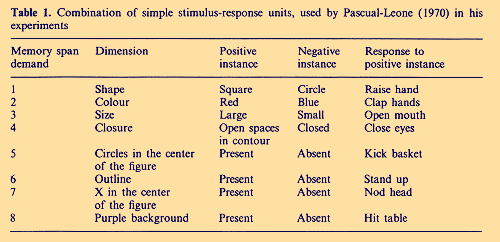 The experimental setting and instructions were as follows: Different sets of cards constituted the stimulus material. Every pair of cards illustrated a simple stimulus-response unit of a given level (see Table 1). Experimenter and subject set facing each other across a table. The task was introduced as a spy game. Experimenter would teach subject a code and when he knew it well, experimenter would send him some secret messages. The whole series was repeated until the subject`s motor responses were without error. When the subject had learned his repertoire the second step was introduced. A new randomly ordered set of cards was presented, exhibiting compound stimuli of all possible combinations previously learned by the subject. The subject`s task was to respond to any recognised stimulus. Cards were presented manually and the exposure time was fixed at 5 sec but the subject had free time for responding. Pascual-Leone`s application (1970; p. 318) of Bose-Einstein statistics to his experimental data seems to be especially important. If a subject has a memory span of 5 and it has to keep in mind a memory set of 5 elements, he cannot arrange element 1 corresponding to span or "attention space" 1, element 2 to span 2 and so on. This will be impossible. Because access to chunks in working memory is random, the available energy quanta are not distinguishable and have to be defined as bosons (i.e. indistinguishable quanta; in contrast to Case & Serlin, 1979, who used distinguishable quanta for modeling the same experiments). The probability distribution of the random variable x (i.e. the number of different, responses produced by the subject) can be calculated on the basis of the combinatorics of the total number c of cues in the stimulus compound (i.e. the span demand of the task; compare Table 1) and the available energy quanta (bosons) n. By applying the Bose-Einstein occupancy model of combinatorics (formula 1)
to his learning experiments with children of different age, Pascual-Leone obtained a very good agreement between empirical probabilities Pe (x)` and Bose-Einstein predicted theoretical probabilities Pt (x) (see Table 2).
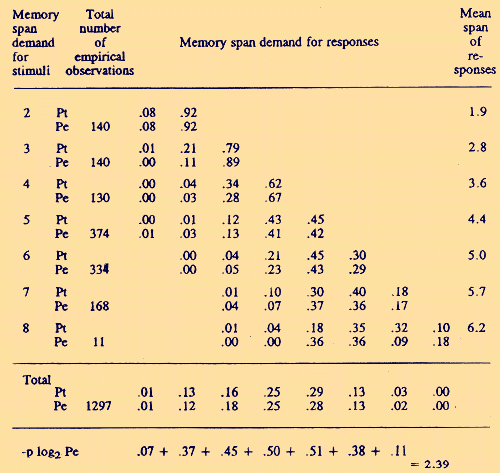 As it seems, the deeper meaning of this astounding agreement between a prediction based on a formula of quantum statistics and an outcome of a psychological experiment has never been discussed seriously. But it should (Weiss, 1992b). Now we try to extend Pascual-Leone`s theory and results: We have added the last row in Table 2, showing the corresponding -p log2 Pe (x). The information entropy H of a system of indistinguishable particles distributed over occupation number n equals (Yu, 1976).
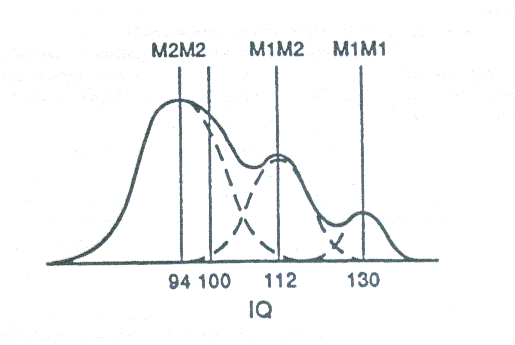
The sum of logarithms to the base 2 of the probabilities that the state n is occupied is 2.39 (see Table 2, last row). For 11-year-olds there are 8 possible quantum states (i.e. the maximum of memory span equals the maximum of such states), hence 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 36. By multiplying 36 with 2.4 we get for this sample of subjects a mean information entropy H of 86.4 bits. A mean IQ of 119 for 11.8 year-olds corresponds in performance to an adult IQ of 102 for about 40-year-olds. In tables of IQ test results edited by Lehrl et al. (1991) and based on concepts of information theory (see below), we read for this age and IQ 102 a short-term memory storage capacity of 84 bits. Two approaches with seemingly completely differing theoretical starting points lead on the absolute scale of information entropy to practically the same result. For Pascual-Leone`s data the latter result was even obtained after applying quantum mechanics twice in series, for calculating Bose-Einstein statistics (by Pascual-Leone himself and formula (1)) and information entropy (by formula2). To understand the message of all this, we must explain in the following the theoretical background of the so-called Erlangen school (Eysenck, 1986; 1992; Guthke, 1993; Jensen, 1993). Already in 1959 Frank (see Lehrl & Fischer, 1990) had claimed that cognitive performance to be limited by the channel capacity of short-term memory. He argued that the capacity H of short-term memory (measured in bits of information) is the product of the processing speed S of information flow (in bits per second) and the duration time D (in seconds) of information in short-term memory absent rehearsal. Hence
According to Frank (1985) the mean channel capacity of IQ 130 is 140 bits, 105 bits of IQ 112, and 70 bits of IQ 92. see: The Basic Period of Individual Mental Speed (BIP) As well known, processing speed can be operationalised in test batteries by sets of elementary cognitive tasks measuring choice reaction time or speed of mental rotation, by scanning information in short-term memory, or by measuring perceptual speed testing inspection time or time to escape masking or reading rate. Such elementary cognitive tasks permit the measurement of individual differences while minimising variance attributable to specific knowledge and acquired intellectual skills and problem-solving strategies. Elementary cognitive tasks (compare Jensen, 1987) are devised to reflect individual differences in information processes rather than in the specific content of information. Elementary cognitive tasks are such simple mental tasks that virtually everyone can perform them correctly and easily. Individual differences in elementary cognitive processes can be assessed in terms of the time required to perform elementary cognitive tasks. Every cognitive task, such as a single item in an IQ test, involves three main categories of abilities that determine successful or unsuccessful performance: (a) information processing abilities, (b) task-relevant knowlegde and (c) a program or strategy. There is probably no task above the level of conditioned reflexes that is so simple as not to involve all three of these features. However, it is possible to devise tasks that drastically minimise variance with respect to knowledge and strategy aspects. Test reliability of all these elementary cognitive tasks is heavily dependent upon the degree of automatisation. Automatisation refers to the decrease in conscious effort or focus of attention in the performance of a task or certain task components usually as a result of extensive practice and overlearning, respectively. Automatisation of a skill greatly reduces its demands on short-term memory. For example, most of us had the experience of learning to drive a car. In the early stages, it took all of our "attentional resources" (just another expression for the capacity of working memory) to shift gears, steer, use the brake, and attend to traffic all at the same time. We could not carry on a conservation or listen attentively to the car radio, or think about other problems while performing the essential coordinated tasks in driving a car. After enough practice, however, these essential skills become automatised to such a degree that one is not even aware of performing them, thereby leaving one`s mind to be almost fully occupied by other things. For an experienced driver a sequence of tasks becomes a new unity which occupies only one element of memory span, for a famous mathematician (Weiss, 1994, 1995) such a superchunk can even be a logical chain of such a length and a lot of ramifications that ordinary people will have the greatest difficulty to understand the resulting conclusions. In contrast to automatic processing, controlled processing of information demands the individual`s focused attention, requires conscious mental effort, is relatively slow, and deals with information input sequentially, being able to handle only very limited amounts of information simultaneously, or in parallel. Controlled processing may crowd the full capacity of short-term memory. It is characteristic of novel problem solving and the learning of new knowledge or skills. Each new step in learning complex knowledge or skills makes great demands an the limited capacity of working memory. It is largely automatisation of prerequisite knowledge and skills that makes it possible for experts to learn something new in their field of expertise much easier and faster than would be possible for novices, regardless of their IQs. Learning curves show a directionally consistent and smooth change in level of performance with practice only when they are group curves based on the average of a number of individual learning curves. Changes in an individual`s performance throughout practice are comparatively erratic, yielding a rather saw-toothed record of gains and losses from trial to trial, although a smoothed curve can usually be fitted to these erratic data points to reveal an overall gradual improvement in performance as a function of amount of practice (compare Jensen, 1988). The first experimental approach to determine mental processing speed (compare also Kail & Salthouse, 1994) in bits per second was accomplished by Naylor (1968). His method of testing enabled the subjects to present to themselves a stimulus which remained as long as they kept a finely balanced switch depressed. The stimuli were digits between 1 and 9 or numbers between 1 and 32 presented singly or in groups of two, three, four, or five. By this procedure the time was measured until the signs were perceived by the subjects. The information content of one digit of the repertoire of nine possibilities was 2 3.17 = 9. That is 3.17 bits. To recognise one of the 32 possibilities (= 25) was equal to 5 bits. The processing speed of 42 young university students was 21.4 bits per second; for 105 adults who were 60-69 years old, 14.2 bits per second. - Harwood and Naylor (1969) measured not only the time between stimulus and reaction but also the amount of stimulus information. This is the prerequisite for the more striking observation (by Lehrl & Fischer, 1990) that the results (in bits/s) are numerically equal although the repertoires if signs differ. The measurement of stimuli and reaction in terms of the information unit (the bit) und physical time will only reveal properties of the subject if the information content of the objective repertoire agrees with that of the subjective repertoire. When a repertoire of signs (such as letters, digits or chunks) is overlearned, independently presented signs, whether of sense or nonsense in common usage, have the same objective as subjective information. Instead of applying one of the elementary cognitive tasks already mentioned, Lehrl et al. (1991) operationalised Frank`s (see 1985) concept of short-term memory storage capacity (in bits) by testing memory span and reading rate. Forward memory span was assessed in the usual way: The experimenter read a series of digits at the rate of one number per second and asked the subject to repeat the digits exactly as heard. The series ranged from three to nine digits in length and were presented in increasing order. The maximum of correct responses of a determined length (i.e. memory span) corresponds with the duration time D (in seconds) of information in short-term memory. Processing speed (in bits per second) was operationalised (Lehrl et al., 1991) by letter reading or number reading. Letter reading consists of four cards. In the middle of each card is a line of 20 independent letters, having phonetically only one syllable. Either in the German or English basic version the first card was:
u n r z t r f e p k b v d s n i l m r
The subject is simply asked to read a series of mixed up letters in an undertone as quickly as possible. As soon as the testee begins to speak, the stopwatch is started. The time from the first to the last spoken letter is measured. It should be documented in tenths of a second, e.g. 7.3 s. Then the next of three similar cards with other letter is given. The total procedure takes about 1- 3 min. Only the best time counts. When evaluating the raw scores it must be remembered that a subject can only perform full binary decisions. Therefore, the recognition of a letter out of the repertoire of 27 letters, which theoretically has an information content of 4.7 bits (27 = 24.7) needs five binary decisions. Since each letter contains 5 bits of information, the 20 letters contain 100 bits. This is divided by the time of reading to obtain the amount of information processed in a second S (bits/s). For example, if the best time of a testee is 7.3 s, then S = 100/7.3 (bits/s) = 13.7 bits/s. By standardising letter reading on adults, normative data are available (see Table 3; column mental speed). SPAN AND SCAN AS TWO SIDES OF THE SAME COIN Forward memory span D can be predicted on the basis of the number of simple words which the subject can read out in 1.8 seconds (Baddeley, Thomson, & Buchanan, 1975). Regardless of the number of syllables, any subject was able to recall as many words as he could read in 1.8 s. This result of an empirical investigation by Baddeley et al. can easily be confirmed by the normative data from Lehrl et al. (1991, p. 35). For example, for IQ 100 holds: The 20 letters of their reading task are read in 6.6s; x (memory span) corresponds to 5.4. Now we can calculate x = 6.6s x 5.4 / 20 = 1.8s. (Lehrl et al. were not aware of the findings by Baddeley et al.) In a classical metaanalysis of a large number of empirical studies, Cavanagh (1972) came to the conclusion: "Span and processing rate are both measures of the same memory system. ... The greater the memory span, the faster the processing rate. ... The time required to process a full memory load is a constant, independent of the type of material stored." However, this relationship between span and speed does only hold interindividually and does not hold, if the study is done within the same individuals (or interindividually within a very restricted range of IQ). We remember Pascual-Leones`s experiments (1970), Processing speed increases throughout childhood and adolescence, reaches a peak in young adulthood, and declines slowly thereafter (see for a review, Kail & Salthouse, 1994). Kail and Salthouse, who tend to see memory span subordinate to processing speed and are speaking of "the concept of mental capacity or processing resources" are well aware, however, and agree with our point of view that this general mental capacity (1994; p. 202) "enables or enhances cognitive processing such that performance in many cognitve tasks is improved when greater amounts of the resource are available" and that this capacity "is not local or specific in the sense that that it is restricted to a small number of highly similar cognitive tasks, but instead is relevant to a broad range of cognitive processes." And Kail and Salthouse add, that these aspects of capacity "have generated a number of specific theories concerning the nature of mental capacity. Most of the proposals rely on metaphors of space, energy, or time. That is, space limitations correspond to restrictions on the size of the computational or working memory region available for processing, energy limitations correspond to attentional fuel restrictions, and time limitations refer to restrictions imposed by tradeoffs between the rate at which information can be processed and the rate at which it becomes available through decay, interference or some other mechanism. These metaphors are not necessarily independent because it is clearly quite possible that aspects of space, energy, and time are interrelated, and in certain circumstances may interchangeable. For example, if working memory is dynamic and needs periodic refreshing, then the capacity of working memory will be determined by the time or energy for available for refreshing. Conversely, if the amount of workspace available for computation is limited, more swapping of information to and from long-term memory will be necessary and the time for most activities will increase. In a similare manner, time and energy may be interchangeable because increased energy may contribute to faster time, and vice versa." Inferring from the near perfect interindividual correlation between span and speed, Nicolson (1981) interpreted Baddeley`s et al. (1975) results as Memory span = capacity x processing speed + constant. It is a pity, but this is not the correct solution. If we solve equation (3) by Frank (see 1985; or Jensen, 1993) for memory span D we get
that means the capacity of working memory (in bits) must be divided by the scan rate (in bits/s) in order to get forward memory span. Hitch et al. (1989) assessed the relationship between memory span and oral reading rate among groups of children aged 8 and 11. Span was estimated on the basis of a word display time of 1.2s (and not 1s as by Lehrl et al., 1991). For the determination of reading rate the subjects had to read aloud, as quickly as possible, lists of 16 words. For each subject, mean time to read was converted into a measure of reading rate (words per second). The empirical data fitted a straight line. The equation of the regression line is
Memory span = 1.68 (oral reading rate) + 0.71
For articulation rate (words per second), the result was
Memory span = 1.20 (articulation rate) + 1.14
From the very beginning of mental testing at the turn of the last century simple word or digit span has been a subtest of many test batteries and has remained such a subtest of IQ measurement until now. In view of the importance of general intelligence for complex real world cognition, we cannot follow any argument that span should be no good predictor for such complex cognition. However, we agree, that from the stochastic nature of span (compare Table 2) follows a relatively low test-retest-reliability. Nevertheless, testing of span has remained a subtest of many IQ tests because of its extreme shortness. In fact, formula (3) is the formula of the shortest test of general intelligence (Lehrl et al., 1991) all over the world. But, of course, the tradeoff of shortness is a lower validity. The overall importance of reading speed in everyday life and as an indicator of processing speed is even more obvious. "4-year-old children process information about three times more slowly than adults, whereas 8-year-olds process information twice as slowly as adults. This pattern of change is found across a wide range of perceptual and cognitive tasks. With increasing age, children name familiar objects more rapidly, and these naming times are related to reading ability.... The results are consistent with the view that times to name these stimuli are determined by a global mechanism that limits the speed with which most cognitive processes are executed", conclude Kail and Hall ( 1994), and add: "There is substantial age-related change in working memory, and greater memory capacity is associated with greater reading recognition skill." According to Carver (1990), the same comprehension processes underlie both reading and auding, so the central process for understanding spoken or written language is called "rauding" by Carver. "In rauding theory, thinking rate is called cognitive speed. The cognitive speed of an individual acts as a governor for rauding rate. Cognitive speed can be measured using tasks that involve naming symbols, such as letters or digits. ... An individual`s cognitive speed seems to act as a speed limit for the rauding process. When individuals go faster than the limit set by their cognitive speed they no longer are spending the time necessary to operate successfully the three primary components of the rauding process - lexical access, semantic encoding, and sentential integration. So, the rauding rate is limited by their own cognitive speed. The fastest rate that individuals can successfully operate their rauding rate is limited by their thinking rate" (Carver, 1992; p. 90). Consequently, there is an inverse relationship between the length of words and their frequencies of usage. According to Zipf (1949; p. 136), this relationship can be desribed by the equation r x f = C, in which r refers to the word`s rank and f to its frequency of occurence; C is the length of a word. Even the approximate optimum size  of the vocabulary of a given individual can be understood as a function of his memory span n. The equation for the underlying General Harmonic Series is as follows
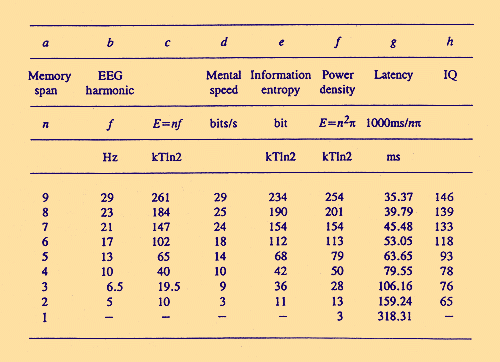
in which p is the value when we view a set of rank-frequency data. Equation (5) describes any set of rank-frequency data whose points fall on a straight line on doubly logarithmic paper. In this case the size of memory span n will be the antilog of the x-intercept, the size of F will be the antilog of th y-intercept; the size of p will be the result of dividing the y-intercept by the x-intercept (for more details, see Zipf, 1949; p. 130ff.). In such a way even the capacity of long-term memory can be understood as a function of memory span. To estimate the amount of this capacity in bits, should be the next logical step. During the last decades a number of authors have claimed not only correlations between span and speed, but also with electrophysiological variables of the EEG. We have already reviewed the arguments and evidence pro and contra such correlations in detail (Weiss, 1989, 1992b), and we will restrict ourselves here to the most pertinent facts. Our aim is to clarify the background of the congruence between Pascual-Leone`s empirical findings (1970) and results on the basis of information theoretical approaches (especially such as by Lehrl et al., 1991). In 1935, Gibbs, Davis, and Lennox had documented that patients (sample size was 55) with petit mal epilepsy show, in all cases during seizures, an outburst of spike waves of great amplitude at a frequency of about 3/s. Now this finding is part of our confirmed knowledge and can be read in every textbook on EEG or epilepsy. From this in 1938, Liberson (see 1985) had drawn the conclusion that all significant channels in EEG could be n multiples of one fundamental frequency of about 3.3 Hz. According to his empirical data the number of these multiples (harmonics) is nine as the maximum of memory span (see Table 3). Assuming these numbers one to nine to be quanta of action (as Pascual-Leone, 1970, did), we (compare Weiss, 1992b) again obtain a relationship between the classical formulae of quantum statistics and empirical results of both EEG and psychometric research
Assuming the numbers 1 to 9 of memory span to be equivalent of harmonics in the sense of wave theory, the power spectral density E is given by the eigenstate energy-frequency relationship
where f is frequency. According to thermodynamics, the measurement of 1 bit of information entropy requires a minimum energy of 1 kT x ln2, where k is Boltzmann`s constant and T is absolute temperature. (Of course, this cannot mean that the brain works with this minimum of energy. The relationship, suggested by Table 3, should hold for a macroscopic analogon, whatever it may be.) During the duration of 1 perceptual moment 1 bit of of information is processed (Lehrl & Fischer, 1990) per harmonic. That means that 1 break of symmetry and 1 phase reversal after each zero-crossing of an EEG wave corresponds with a possible 1 bit decision between two alternatives. Consequently, each degree of freedom and of translation (this refers to mathematical group theory underlying both mental rotation and quantum mechanics; compare Goebel, 1990) to an energy of kT/2 or its macroscopic analogon. Empirical analysis (Weiss, Lehrl & Frank, 1986) shows that Liberson`s (1985) fundamental is lower thant 3.3 Hz and in the range between 3.1 and 3.3 Hz, i.e. near 3.14 Hz. Therefore, in Table 3 we have written for simplification npHz. Because the frequency of harmonics can be expressed as npHz, for the expected latencies of harmonics follows 1000 ms/n and for power density follows E = n²p (kT x ln2). The physical term power is used because it is a measure of the ability of waves at frequency f to do work. The power spectrum to the EEG describes the total variance in the amplitudes due to the integer multiples of the fundamental frequency (i.e. the first harmonic 1 ). In order to calculate power density in this way, the waveform must be squared and then integrated for the duration of its impulse response, i.e. the duration of the transient of 1 complete wave packet containing all the harmonics of the memory span of a given subject. Calculating the energy E of the impulse response in this way, we must again obtain the energy E, given in Table 3. What in an evoked response of EEG can be found, is not only the response to a given stimulus, a given signal, but also a specific impulse response dependent upon the relatively constant brain energy metabolic state of a given individual (for more details see Weiss 1992a, 1992b, 1995). When a stimulus is fed into the brain, the short-term memory wave packet immediately operates on this input, and the result is the corresponding output signal (a thought). The mathematical relationship is that the output is equal to the convolution (time reversal) of the input with the short-term memory impulse function (Crick, Marr & Poggio, 1981). Time reversal (i.e. the concept of convolution in terms of communication theory) explains why the higher harmonics occur first after a stimulus. Higher IQ subjects have not only a higher memory span, but consequently also more complex waveforms of EEG than lower IQ subjects. The most extreme compression of information is represented by the eigenvalues of the power spectrum. There are as much eigenvalues of a spectrum as are harmonics. Each eigenvalue of event related electrocortical potentials is repressented by a crossing of the zero-volt-line. In 1989 Weiss predicted, that up to the P300 the number of these zero-crossings is identical with the maximum of memory span. In view of the fact, that the correlation between EEG parameters and memory span (Polich, Howard, & Starr, 1983) was well known for about a decade, it is surprising that this conclusionn has not been drawn earlier. Already in 1959 Burch (cited from Saltzberg & Burch, 1971) had found that "the parameters ... of the power spectral density ... can be estimated in a completely adequate way without the necessity of performing squaring and integrating operations but simply by counting the zero crossings." Barrett and Eysenck (1994), testing the prediction, found in a subsample a mean IQ of 105 corresponding to a mean of 2.9 zero-crossings, in a second subsample a mean IQ of 107 corresponding to 3.5 zero-crossings, in a third a mean IQ of 110 corresponding to a zero-cross count of 3.9. However, the condition of the experiments did not fulfill the requirements (Weiss, 1989) for a proper testing of the prediction. For example, stimulus duration was 30 ms, but should not longer than 4 ms. Barrett (by personal communication) has acknowledged these shortcomings, and he is reanalysing his data. Moreover, by considering the content of Table 2, we have to modify the prediction: The number of zero-crosses is the upper bound of the memory span of an individual. In testing this prediction, averaging the evoked responses is of no use. Each single response should be analysed separately. Theoretically, the distribution of zero-cross counts of all single responses should fit Bose-Einstein statistics. The empirical findings resulting from very different starting points, by Pascual-Leone (1970) in the wake of Piaget`s tradition, by the German school of information psychology (Lehrl & al., 1991) and by EEG results support our argument, that memory span has to be understood as the quantum of action action of thought. In fact, this quanta of action represent macroscopic ordered states in the sense of quantum mechanics (Weisman, 1988; Marshall, 1989). If we get from different starting points and different empirical background always the same result, and if we get from the different formulae (2), (3) and (6) always the same amount E of general mental power, we should no longer speak of a mere hypothesis, but of an underlying theory. What we have outlined is a fundamental theory, closing the gap between cognitive and differential psychology and psychophysiology, respectively. A quantifying theory, which is more than a mere "metaphore of space, energy, or time" (compare Kail & Salthouse, 1994, already quoted above) and therefore worth to become a component of mainstream science.
REFERENCES
Promolibro.
A theory of intelligence: I. Span
and the complexity of stimulus control. Intelligence, 1, 127-150.
Word length and the structure of short-term memory.
Journal of Verbal Learning and Behavior, 14, 575-589.
The relationship between evoked potential component amplitude, latency, contour length,
variability, zero-crossings, and psychometric intelligence. Personality and individual
Differences, 16, 3-32.
Working memory capacity as long-term memory activation: an individual-differences approach.
Journal of Experimental
Psychology: Learning, Memory and Cognition, 19, 110-1114.
Intellectual Development: Birth to Adulthood. Orlando: Academic.
A new progressing model for predicting performanc
Pascual-Leone`s test of M-space. Cognitive Psychology, 11, 308-326.
Relation between the immediate memory span and the
memory search rate. Psychological Review, 79, 525-530.
Cognitive development and the growth of capacity: issues
in neoPiagetian theory. In J. T. Enns (Ed) The Development of Attention:
Research and Theory. Amsterdam: Elsevier, pp. 263-287.
An information-processing approach to understanding the visual cortex. In F. O. Schmitt,
E. G. Worden, G. Edelman & S. C. Dennis (Eds). The Organization of the Cerebral Cortex.
Cambridge: MIT Press, pp. 505-535..
Memory span: sources of individual and developmental
difference. Psychological Bulletin, 89, 63-100.
The theory of intelligence and the psychophysiology
of cognition. In R. J. Sternberg (Ed) Advances in the Psychology of
Human Intelligence, Vol. 3. Hillsdale, NJ: Erlbaum, pp. 1-34.
Speed of information processing, reaction time, and
the theory of intelligence. In P. A. Vernon (Ed) Speed of Information-
Processing and Intelligence. Norwood: Ablex, pp. 21-67.
The one and the many. In D. K. Detterman (Ed) Current Topics
in Human Intelligence, Vol. 2: Is Mind Modular or Unitary? Norwood: Ablex,
pp. 83-116.
Is intelligence measurable and is it inherited? Folia
humanistica, 23, 671-691.
Mathematical disabilities: cognitive, neuropsychological, and
genetic components. Psychological Bulletin, 114, 345-362.
The electroencephalogram in epilepsy and in conditions of impaired consciousness. Archive of
Neurology and Psychiatry, 34, 1133-1148.
The mathematics of mental rotations. Journal of Mathematical Psychology, 34, 435-444.
Intelligenzmessung. In A. Schorr (Ed) Handwörterbuch der Angewandten Psychologie.
Bonn: Deutscher Psychologie-Verlag, pp. 356-361.
The Development of Thought. Hillsdale, NJ: Erlbaum.
Rates and information transfer in elderly subjects. Australian Journal of Psychology, 21,
127-136.
P300 latency and memory span development. Developmental Psychology, 21,283-289.
A Piagetian test of general intelligence. Developmental Psychology, 21, 872-877.
Mental chronometry in the study of learning disabilities.
The Mental Retardation and Learning Disability Bulletin, 15, 67-88.
The relationship between learning and intelligence.
Learning and Individual Differences, 1, 37-62.
Why is reaction time correlated with psychometric g? Current Directions in Psychological Science, 2, 53-56.
A capacity theory of comprehension:
individual differences in working memory. Psychological Review, 99, 122-149.
Lehrl, S., & Fischer, B. (1990).
A basic information psychological parameter (BIP) for the reconstruction of concepts of intelligence. European Journal of Personality 4, 259-286 - see: The Basic Period of Individual Mental Speed (BIP)
Geistige Leistungsfähigkeit. Theorie und Messung der biologischen Intelligenz mit dem Kurztest
KAI. Ebersberg: Vless.
Regional spectral analysis of EEG and ' active ` and 'passive ` intelligence.
In D. Giannitrapani, The Electrophysiology of Intellectual Functions. Basel: Karger,
pp. 153-176.
Consciousness and Bose-Einstein condensates. New Ideas in Psychology, 7, 73-83.
The magical number seven, plus or minus two: some limits on our capacity for processing
information. Psychological Review, 63, 81-97.
Perception times and rates a a function of the qualitative and quantitative structure of the
stimulus. Australian Journal of Psychology, 20, 165-172.
The relationship between memory span and processing speed. In M. P. Friedman,
J. P. Das & N. O' Connor (Eds) Intelligence and Learning. London: Plenum, pp. 179-183.
A mathematical model for the transition rule in Piaget`s developmental stages.
Acta Psychologica, 32, 301-345.
Organismic processes for neo-Piagetian theories: a dialectical causal account of cognitive
development. International Journal of Psychology, 22, 531-570.
The theory of stages in cognitive development. In D. R. Green (Ed) Measurement and Piaget.
New York: Mc Graw Hill, pp. 1-11.
P300 latency correlates with digit span. Psychophysiology, 20, 665-669.
Interactions between basic capacity and strategies in children`s memory:
Construction of a developmental paradigm.
Cahiers de Psychologie Cognitive, 9, 471-504.
Period analytic estimates of moments of the power spectrum:
a simplified EEG time domain procedure.
Electroencephalography and Clinical Neurophysiology, 30, 568-570.
Information processing capacity and the problem of horizontal décalage:
a demonstration using combinatorial reasoningtasks.
Child Development, 48, 28-37.
Das unmittelbare Behalten. Göttingen: Hogrefe.
Weisman, H. S. (1988). Toward a quantum mechanics of intelligence. In J. W.
Jamieson (Ed) Essays on the Nature of Intelligence. Washington: Cliveden,
pp. 25-49.
From memory span and mental speed toward the quantum mechanics of intelligence. Personality and individual Differences, 7, 737-749.
Weiss, V. (1989). From short-term memory capacity toward the EEG resonance code. Personality and individual Differences, 10, 501-508.
The spatial metric of brain underlying the temporal metric
of EEG and thought. Gegenbaurs morphologisches Jahrbuch, 136,79-87.
Major genes of general intelligence. Personality and individual differences, 13, 1115-1134.
The relationship between short-term memory capacity and EEG power spectral density. Biological Cybernetics, 68, 165-172.
Weiss, V. (1994).Mathematical giftedness and family relationship . European Journal for High Ability, 5, 59-67.
Psychogenetik der Intelligenz. Dortmund: Modernes Lernen.
Optics and Information Theory. New York: Wiley.
|